- FONCTIONS ANALYTIQUES - Fonctions d’une variable complexe
- FONCTIONS ANALYTIQUES - Fonctions d’une variable complexeOn se propose, dans ce premier article, d’exposer, avec des démonstrations quasiment complètes, les résultats les plus élémentaires de la théorie des fonctions analytiques d’une variable complexe; les deux derniers chapitres sont consacrés à quelques résultats sans démonstration. Historiquement, l’extension au cas complexe de nombreuses fonctions classiques a été réalisée par l’intermédiaire des développements en série; les séries entières restent à la base de l’étude locale des fonctions analytiques. Avec l’introduction de l’intégrale curviligne, on peut aborder des problèmes globaux, comme la recherche des primitives, qui font apparaître des conditions de nature «géométrique» ou, plutôt, topologique, imposées aux ouverts du plan complexe; les représentations intégrales de Cauchy sont à la base du calcul des résidus, qui a d’innombrables applications pratiques.On a passé sous silence les résultats relatifs aux fonctions harmoniques de deux variables, qui ne sont autres que les parties réelles de fonctions analytiques, en renvoyant à l’article POTENTIEL ET FONCTIONS HARMONIQUES.1. Séries entièresLa définition et l’étude des fonctions analytiques reposent sur la notion de série entière, c’est-à-dire de série de la forme:
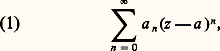 où a et les a n sont des nombres complexes donnés; on dit qu’une telle série (1) est une série entière de centre a et de coefficients a n .On dit que la série (1) converge normalement dans un ensemble K 說 C si la série des modules de ses termes est uniformément convergente pour z 捻 K. Rappelons qu’il suffit pour cela qu’il existe une série numérique convergente de terme général 見n telle que |a n (z 漣 a )n | 諒 見n pour tout n 捻 N et z 捻 K.On désigne, dans ce qui suit, par D (a , r ) et D 漣 (a , r ) les disques ouvert et fermé de centre a et de rayon r , c’est-à-dire les ensembles de nombres complexes z tels que |z 漣 a | 麗 r et |z 漣 a | 諒 r respectivement.ConvergenceÉtudions l’ensemble des nombres complexes z pour lesquels la série (1) est convergente. Posant Z = z 漣 a pour simplifier, on se ramène, par une translation, à une série entière:
où a et les a n sont des nombres complexes donnés; on dit qu’une telle série (1) est une série entière de centre a et de coefficients a n .On dit que la série (1) converge normalement dans un ensemble K 說 C si la série des modules de ses termes est uniformément convergente pour z 捻 K. Rappelons qu’il suffit pour cela qu’il existe une série numérique convergente de terme général 見n telle que |a n (z 漣 a )n | 諒 見n pour tout n 捻 N et z 捻 K.On désigne, dans ce qui suit, par D (a , r ) et D 漣 (a , r ) les disques ouvert et fermé de centre a et de rayon r , c’est-à-dire les ensembles de nombres complexes z tels que |z 漣 a | 麗 r et |z 漣 a | 諒 r respectivement.ConvergenceÉtudions l’ensemble des nombres complexes z pour lesquels la série (1) est convergente. Posant Z = z 漣 a pour simplifier, on se ramène, par une translation, à une série entière: de centre O.Théorème 1. Soit R (éventuellement égal à 0 ou à + 秊) défini par la formule d’ Hadamard :
de centre O.Théorème 1. Soit R (éventuellement égal à 0 ou à + 秊) défini par la formule d’ Hadamard :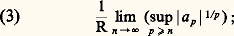 alors, pour tout r 麗 R, la série (2) converge normalement dans le disque fermé D 漣(0, r ) (en particulier, cette série converge absolument pour |Z| 麗 R) et diverge pour |Z| 礪 R.Ce nombre R est appelé le rayon de convergence de la série entière (2) et le disque ouvert correspondant D(0, R), qui est éventuellement vide ou égal au plan complexe tout entier, est appelé le disque de convergence de cette série. Remarquons que le théorème n’affirme rien pour |Z| = R; toutes les circonstances peuvent se rencontrer: divergence en tout point de ce cercle, convergence avec ou sans convergence absolue en certains points, convergence partout (cf. infra , Principe des zéros isolés ).Il faut indiquer la démonstration du théorème 1. Supposons d’abord R 礪 0 et soit r 麗 R: choisissons 福 tel que r 麗 福 麗 R. D’après (3), on a:
alors, pour tout r 麗 R, la série (2) converge normalement dans le disque fermé D 漣(0, r ) (en particulier, cette série converge absolument pour |Z| 麗 R) et diverge pour |Z| 礪 R.Ce nombre R est appelé le rayon de convergence de la série entière (2) et le disque ouvert correspondant D(0, R), qui est éventuellement vide ou égal au plan complexe tout entier, est appelé le disque de convergence de cette série. Remarquons que le théorème n’affirme rien pour |Z| = R; toutes les circonstances peuvent se rencontrer: divergence en tout point de ce cercle, convergence avec ou sans convergence absolue en certains points, convergence partout (cf. infra , Principe des zéros isolés ).Il faut indiquer la démonstration du théorème 1. Supposons d’abord R 礪 0 et soit r 麗 R: choisissons 福 tel que r 麗 福 麗 R. D’après (3), on a: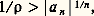
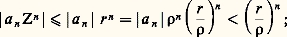 ainsi le terme général de (2) est majoré en module pour Z 捻 D 漣(0, r ) par le terme général d’une série géométrique convergente, d’où la convergence normale. Réciproquement, soit |Z| 礪 R. D’après (3), il existe alors pour n une infinité de valeurs telles que |a n |1/n 礪 1/|Z|, soit |a n Zn | 礪1; ainsi le terme général de la série (2) ne tend pas vers 0 et cette série diverge.Pour trouver un rayon de convergence, on utilise rarement la formule (3), dont l’intérêt est surtout théorique, mais on étudie, suivant les valeurs Z, la convergence absolue de la série (2) en utilisant les critères classiques [cf. SÉRIES ET PRODUITS INFINIS]. Ainsi, la série de terme général n ! z n a un rayon de convergence nul (critère de d’Alembert); la série:
ainsi le terme général de (2) est majoré en module pour Z 捻 D 漣(0, r ) par le terme général d’une série géométrique convergente, d’où la convergence normale. Réciproquement, soit |Z| 礪 R. D’après (3), il existe alors pour n une infinité de valeurs telles que |a n |1/n 礪 1/|Z|, soit |a n Zn | 礪1; ainsi le terme général de la série (2) ne tend pas vers 0 et cette série diverge.Pour trouver un rayon de convergence, on utilise rarement la formule (3), dont l’intérêt est surtout théorique, mais on étudie, suivant les valeurs Z, la convergence absolue de la série (2) en utilisant les critères classiques [cf. SÉRIES ET PRODUITS INFINIS]. Ainsi, la série de terme général n ! z n a un rayon de convergence nul (critère de d’Alembert); la série: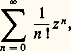 dont la somme est la fonction exponentielle complexe (cf. EXPONENTIELLE ET LOGA- RITHME, chap. 4), converge absolument pour tout z et a donc un rayon de convergence infini. Les séries:
dont la somme est la fonction exponentielle complexe (cf. EXPONENTIELLE ET LOGA- RITHME, chap. 4), converge absolument pour tout z et a donc un rayon de convergence infini. Les séries: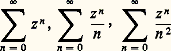 ont chacune un rayon de convergence égal à 1, mais ont des comportements très différents pour |z | = 1: la première ne converge en aucun point de ce cercle puisque alors son terme général est de module égal à 1; la deuxième converge (mais pas absolument) en tout point de ce cercle différent de 1 et diverge pour z = 1; la troisième converge normalement pour |z | = 1.Fonctions analytiquesSoit U un ouvert du plan complexe et f : UC une fonction à valeurs complexes. On dit que f est analytique ou holomorphe dans U si elle est développable en série entière au voisinage de tout point de U, c’est-à-dire si, pour tout a 捻 U, il existe une série entière de centre a dont la somme est égale à f (z ) dans un disque de centre a :
ont chacune un rayon de convergence égal à 1, mais ont des comportements très différents pour |z | = 1: la première ne converge en aucun point de ce cercle puisque alors son terme général est de module égal à 1; la deuxième converge (mais pas absolument) en tout point de ce cercle différent de 1 et diverge pour z = 1; la troisième converge normalement pour |z | = 1.Fonctions analytiquesSoit U un ouvert du plan complexe et f : UC une fonction à valeurs complexes. On dit que f est analytique ou holomorphe dans U si elle est développable en série entière au voisinage de tout point de U, c’est-à-dire si, pour tout a 捻 U, il existe une série entière de centre a dont la somme est égale à f (z ) dans un disque de centre a : Remarquons que les coefficients a n et le nombre r 礪 0 dépendent du point a considéré. A priori le nombre r est inférieur ou égal au rayon de convergence de la série qui figure dans (4). Remarquons que cette série est normalement convergente dans tout disque fermé de rayon assez petit (théorème 1), et, par suite, f est une fonction continue dans U.Voici, en liaison avec ce qui précède, un important exemple de fonction analytique.Théorème 2. La somme d’une série entière est analytique dans son disque de convergence.On se ramène par translation à une série entière de centre O:
Remarquons que les coefficients a n et le nombre r 礪 0 dépendent du point a considéré. A priori le nombre r est inférieur ou égal au rayon de convergence de la série qui figure dans (4). Remarquons que cette série est normalement convergente dans tout disque fermé de rayon assez petit (théorème 1), et, par suite, f est une fonction continue dans U.Voici, en liaison avec ce qui précède, un important exemple de fonction analytique.Théorème 2. La somme d’une série entière est analytique dans son disque de convergence.On se ramène par translation à une série entière de centre O: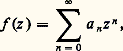 de rayon de convergence R; soit z 0 un point du disque de convergence et posons z = z 0 + (z 漣 z 0). La formule du binôme de Newton donne:
de rayon de convergence R; soit z 0 un point du disque de convergence et posons z = z 0 + (z 漣 z 0). La formule du binôme de Newton donne: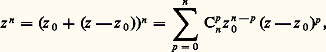 d’où:
d’où: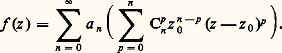 On montre alors que, pour:
On montre alors que, pour: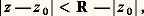 la série double ci-dessus est sommable; on peut donc intervertir les deux signes de sommation, d’où:
la série double ci-dessus est sommable; on peut donc intervertir les deux signes de sommation, d’où: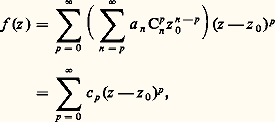
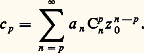 La fonction f est donc somme d’une série entière de centre z 0 dans le disque ouvert D(z 0, R 漣 |z 0|); remarquons que cette série a donc un rayon de convergence R 漣 |z 0|, mais ce rayon de convergence peut être strictement plus grand. Le disque de convergence «déborde» alors du disque de convergence de la série initiale, et cela permet de prolonger la fonction f en une fonction analytique dans la réunion des deux disques (cf. chap. 7).Principe des zéros isolésExaminons maintenant le comportement d’une fonction analytique au voisinage d’un point où elle s’annule.Soit f une fonction analytique dans un ouvert U et a 捻 U un zéro de f . La fonction f est développable en série entière au voisinage de a , c’est-à-dire que l’on a (4) dans un disque D(a , r ) où a 0 = f (a ) = 0. Si tous les coefficients de la série (4) ne sont pas nuls, ce qui aura lieu en particulier si f n’est pas identiquement nulle dans D(a , r ), désignons par a k le premier coefficient non nul; on a alors:
La fonction f est donc somme d’une série entière de centre z 0 dans le disque ouvert D(z 0, R 漣 |z 0|); remarquons que cette série a donc un rayon de convergence R 漣 |z 0|, mais ce rayon de convergence peut être strictement plus grand. Le disque de convergence «déborde» alors du disque de convergence de la série initiale, et cela permet de prolonger la fonction f en une fonction analytique dans la réunion des deux disques (cf. chap. 7).Principe des zéros isolésExaminons maintenant le comportement d’une fonction analytique au voisinage d’un point où elle s’annule.Soit f une fonction analytique dans un ouvert U et a 捻 U un zéro de f . La fonction f est développable en série entière au voisinage de a , c’est-à-dire que l’on a (4) dans un disque D(a , r ) où a 0 = f (a ) = 0. Si tous les coefficients de la série (4) ne sont pas nuls, ce qui aura lieu en particulier si f n’est pas identiquement nulle dans D(a , r ), désignons par a k le premier coefficient non nul; on a alors: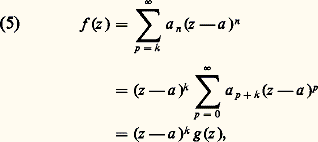 où la fonction g est analytique dans D(a , r ) et g (a ) = a k 0. Le nombre entier k ainsi déterminé s’appelle, par analogie avec le cas des polynômes, l’ordre du zéro a . Puisque la fonction est continue et prend une valeur non nulle en a , il existe un disque D(a , 福) 說 D(a , r ) dans lequel elle ne s’annule pas; ainsi, z = a est le seul zéro de f dans le disque D(a , 福). On a ainsi obtenu le principe des zéros isolés , que l’on peut aussi énoncer ainsi: Soit f une fonction analytique dans un ouvert U; si un point a 捻 U est limite d’une suite de zéros de f , alors f est identiquement nulle dans tout un disque de centre a . Il en résulte aussi que, si la somme d’une série entière de centre a est identiquement nulle dans un disque de centre a , alors tous ses coefficients sont nuls; on en déduit immédiatement l’unicité du développement en série entière d’une fonction analytique au voisinage de tout point.Les résultats précédents sont dits locaux: ils s’appliquent à des disques de rayons assez petits. Pour «globaliser», nous aurons besoin d’introduire une notion topologique qui joue un rôle essentiel dans tout ce qui suit. On dit qu’un ouvert U est connexe s’il ne peut pas s’écrire comme une réunion de deux ouverts non vides disjoints; un ouvert connexe est souvent appelé un domaine . Tout ouvert quelconque du plan est une réunion de domaines deux à deux disjoints appelés les composantes connexes de cet ouvert. La condition de connexité équivaut à ceci: deux points quelconques de U peuvent être joints par une ligne brisée entièrement contenue dans U (fig. 1): supposons d’abord U connexe et soit a 捻 U; désignons par U1 l’ensemble des points de U qui peuvent être joints à a par une ligne brisée située dans U et par U2 l’ensemble des points pour lesquels il est impossible de trouver une telle ligne brisée. L’ensemble U1 est ouvert, car, pour tout point b 捻 U1, il existe un disque D de centre b contenu dans U, et ce disque est en fait contenu dans U1, car tout z 捻 D peut être joint à a par une ligne brisée dans U: il suffit de «rajouter» à la ligne brisée joignant a et b le segment d’origine b et d’extrémité z , qui est contenu dans D, donc dans U. Pour la même raison l’ensemble U2 est aussi ouvert, car, si c 捻 U2, il existe un disque de centre c contenu dans U, et ce disque est contenu dans U2; en effet, s’il contenait un point b 捻 U1, on pourrait joindre a à c par une ligne brisée en rajoutant le segment d’origine b et d’extrémité c à la ligne brisée joignant a à b , ce qui contredit c 捻 U2. Puisque U = U1 聆 U2, et U1 non vide car il contient a , on a nécessairement U2 = 歷. Réciproquement, faisons l’hypothèse que deux points de U peuvent toujours être joints par une ligne brisée située dans U; on va supposer que U peut s’écrire U1 聆 U2, où U1 et U2 sont des ouverts non vides disjoints et aboutir à la contradiction qu’ils ne sont pas disjoints. Soit a 捻 U1 et b 捻 U2; il existe une ligne brisée L 說 U image du segment [0, 1] par une fonction affine par morceaux t 料 塚(t ) d’origine a et d’extrémité b , c’est-à-dire telle que 塚(0) = a et 塚(1) = b . Soit A l’ensemble des t 捻 [0, 1] tels que 塚([0, t ]) 說 U1 et soit 見 la borne supérieure de A; puisqu’il existe un disque ouvert de centre a contenu dans U1, on a 見 礪 0. De plus, 塚( 見) 捻 U1, car, sinon, 塚( 見) appartiendrait à U2 et, puisque U2 est ouvert, il existerait tout un intervalle ] 見 漣 兀, 見] dont l’image par 塚 serait contenue dans U2, en contradiction avec la définition de 見; il suffit donc de montrer que 見 = 1, d’où b = 塚(1) 捻 U1, soit U1 惡 U2 歷. Or, si 見 麗 1, comme 塚( 見) appartient à U1, qui est ouvert, il existerait tout un intervalle [ 見, 見 + 兀 [ dont l’image par 塚 serait contenue dans U1, en contradiction avec le fait que 見 soit la borne supérieure de A.Nous étant ainsi un peu familiarisés avec la notion d’ouvert connexe, on peut énoncer le principe du prolongement analytique. Soit f et g deux fonctions analytiques dans un ouvert connexe U; s’il existe une suite de points distincts z n 捻 U convergeant vers a 捻 U, avec f (z n ) = g (z n ), alors on a identiquement f (z ) = g (z ) dans tout U. Ce principe pourra s’appliquer par exemple si on a f (z ) = g (z ) en tous les points d’une «ligne», ou, de manière encore plus particulière, si f et g sont égales dans un ouvert non vide inclus dans U. C’est la justification correcte du «prolongement des égalités» au domaine complexe: Si deux fonctions analytiques dans un même ouvert connexe U sont égales sur U 惡 R supposé non vide, alors elles sont égales dans U tout entier, ce qui permet d’étendre au champ complexe des formules connues dans le cas réel.Établissons ce principe du prolongement analytique. Soit U1 l’ensemble des points de U au voisinage desquels f 漣 g est identiquement nul, soit U2 son complémentaire dans U. Tout point de U1 est centre d’un disque dans lequel f 漣 g est identiquement nul, et, par suite, tout ce disque est dans U1; ainsi U1 est ouvert et il est non vide, car d’après le principe des zéros isolés, il contient a . Montrons que U2 est ouvert aussi, ce qui montrera, puisque U est connexe, que U2 = 歷. Cela résulte de la continuité en b , ou, si f (b ) = g (b ), du principe des zéros isolés; en effet, si b 捻 U2, f 漣 g n’est pas identiquement nul au voisinage de b , et, par suite, il existe tout un disque de centre b dans lequel b est le seul zéro éventuel de f 漣 g , ce qui entraîne que ce disque est contenu dans U2.2. La dérivation complexeSoit U un ouvert du plan et f une fonction à valeurs complexes définie dans U. On dit que f est dérivable au sens complexe en un point z 0 = x 0 + iy 0 捻 U si l’expression:
où la fonction g est analytique dans D(a , r ) et g (a ) = a k 0. Le nombre entier k ainsi déterminé s’appelle, par analogie avec le cas des polynômes, l’ordre du zéro a . Puisque la fonction est continue et prend une valeur non nulle en a , il existe un disque D(a , 福) 說 D(a , r ) dans lequel elle ne s’annule pas; ainsi, z = a est le seul zéro de f dans le disque D(a , 福). On a ainsi obtenu le principe des zéros isolés , que l’on peut aussi énoncer ainsi: Soit f une fonction analytique dans un ouvert U; si un point a 捻 U est limite d’une suite de zéros de f , alors f est identiquement nulle dans tout un disque de centre a . Il en résulte aussi que, si la somme d’une série entière de centre a est identiquement nulle dans un disque de centre a , alors tous ses coefficients sont nuls; on en déduit immédiatement l’unicité du développement en série entière d’une fonction analytique au voisinage de tout point.Les résultats précédents sont dits locaux: ils s’appliquent à des disques de rayons assez petits. Pour «globaliser», nous aurons besoin d’introduire une notion topologique qui joue un rôle essentiel dans tout ce qui suit. On dit qu’un ouvert U est connexe s’il ne peut pas s’écrire comme une réunion de deux ouverts non vides disjoints; un ouvert connexe est souvent appelé un domaine . Tout ouvert quelconque du plan est une réunion de domaines deux à deux disjoints appelés les composantes connexes de cet ouvert. La condition de connexité équivaut à ceci: deux points quelconques de U peuvent être joints par une ligne brisée entièrement contenue dans U (fig. 1): supposons d’abord U connexe et soit a 捻 U; désignons par U1 l’ensemble des points de U qui peuvent être joints à a par une ligne brisée située dans U et par U2 l’ensemble des points pour lesquels il est impossible de trouver une telle ligne brisée. L’ensemble U1 est ouvert, car, pour tout point b 捻 U1, il existe un disque D de centre b contenu dans U, et ce disque est en fait contenu dans U1, car tout z 捻 D peut être joint à a par une ligne brisée dans U: il suffit de «rajouter» à la ligne brisée joignant a et b le segment d’origine b et d’extrémité z , qui est contenu dans D, donc dans U. Pour la même raison l’ensemble U2 est aussi ouvert, car, si c 捻 U2, il existe un disque de centre c contenu dans U, et ce disque est contenu dans U2; en effet, s’il contenait un point b 捻 U1, on pourrait joindre a à c par une ligne brisée en rajoutant le segment d’origine b et d’extrémité c à la ligne brisée joignant a à b , ce qui contredit c 捻 U2. Puisque U = U1 聆 U2, et U1 non vide car il contient a , on a nécessairement U2 = 歷. Réciproquement, faisons l’hypothèse que deux points de U peuvent toujours être joints par une ligne brisée située dans U; on va supposer que U peut s’écrire U1 聆 U2, où U1 et U2 sont des ouverts non vides disjoints et aboutir à la contradiction qu’ils ne sont pas disjoints. Soit a 捻 U1 et b 捻 U2; il existe une ligne brisée L 說 U image du segment [0, 1] par une fonction affine par morceaux t 料 塚(t ) d’origine a et d’extrémité b , c’est-à-dire telle que 塚(0) = a et 塚(1) = b . Soit A l’ensemble des t 捻 [0, 1] tels que 塚([0, t ]) 說 U1 et soit 見 la borne supérieure de A; puisqu’il existe un disque ouvert de centre a contenu dans U1, on a 見 礪 0. De plus, 塚( 見) 捻 U1, car, sinon, 塚( 見) appartiendrait à U2 et, puisque U2 est ouvert, il existerait tout un intervalle ] 見 漣 兀, 見] dont l’image par 塚 serait contenue dans U2, en contradiction avec la définition de 見; il suffit donc de montrer que 見 = 1, d’où b = 塚(1) 捻 U1, soit U1 惡 U2 歷. Or, si 見 麗 1, comme 塚( 見) appartient à U1, qui est ouvert, il existerait tout un intervalle [ 見, 見 + 兀 [ dont l’image par 塚 serait contenue dans U1, en contradiction avec le fait que 見 soit la borne supérieure de A.Nous étant ainsi un peu familiarisés avec la notion d’ouvert connexe, on peut énoncer le principe du prolongement analytique. Soit f et g deux fonctions analytiques dans un ouvert connexe U; s’il existe une suite de points distincts z n 捻 U convergeant vers a 捻 U, avec f (z n ) = g (z n ), alors on a identiquement f (z ) = g (z ) dans tout U. Ce principe pourra s’appliquer par exemple si on a f (z ) = g (z ) en tous les points d’une «ligne», ou, de manière encore plus particulière, si f et g sont égales dans un ouvert non vide inclus dans U. C’est la justification correcte du «prolongement des égalités» au domaine complexe: Si deux fonctions analytiques dans un même ouvert connexe U sont égales sur U 惡 R supposé non vide, alors elles sont égales dans U tout entier, ce qui permet d’étendre au champ complexe des formules connues dans le cas réel.Établissons ce principe du prolongement analytique. Soit U1 l’ensemble des points de U au voisinage desquels f 漣 g est identiquement nul, soit U2 son complémentaire dans U. Tout point de U1 est centre d’un disque dans lequel f 漣 g est identiquement nul, et, par suite, tout ce disque est dans U1; ainsi U1 est ouvert et il est non vide, car d’après le principe des zéros isolés, il contient a . Montrons que U2 est ouvert aussi, ce qui montrera, puisque U est connexe, que U2 = 歷. Cela résulte de la continuité en b , ou, si f (b ) = g (b ), du principe des zéros isolés; en effet, si b 捻 U2, f 漣 g n’est pas identiquement nul au voisinage de b , et, par suite, il existe tout un disque de centre b dans lequel b est le seul zéro éventuel de f 漣 g , ce qui entraîne que ce disque est contenu dans U2.2. La dérivation complexeSoit U un ouvert du plan et f une fonction à valeurs complexes définie dans U. On dit que f est dérivable au sens complexe en un point z 0 = x 0 + iy 0 捻 U si l’expression: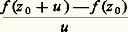 tend vers une limite f (z 0) lorsque le nombre complexe u = s + it tend vers zéro en module (c’est-à-dire lorsque (s , t ) tend vers (0, 0) dans R2); le nombre complexe f (z 0) s’appelle la dérivée de f au sens complexe au point z 0.Équations de Cauchy-RiemannLa condition de dérivabilité complexe au point z 0 peut aussi s’écrire:
tend vers une limite f (z 0) lorsque le nombre complexe u = s + it tend vers zéro en module (c’est-à-dire lorsque (s , t ) tend vers (0, 0) dans R2); le nombre complexe f (z 0) s’appelle la dérivée de f au sens complexe au point z 0.Équations de Cauchy-RiemannLa condition de dérivabilité complexe au point z 0 peut aussi s’écrire: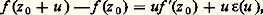
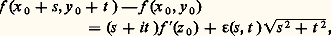 ce qui exprime que la fonction f (x , y ), considérée comme fonction des deux variables réelles x et y , est dérivable (cf. CALCUL INFINITÉSIMAL – Calcul à plusieurs variables, chap. 2) et que:
ce qui exprime que la fonction f (x , y ), considérée comme fonction des deux variables réelles x et y , est dérivable (cf. CALCUL INFINITÉSIMAL – Calcul à plusieurs variables, chap. 2) et que: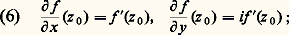 d’où:
d’où: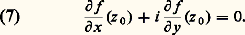 Réciproquement, si f est une fonction dérivable des deux variables x et y satisfaisant à la condition (7), elle est dérivable au sens complexe. Si on pose f (x , y ) = P(x , y ) + i Q(x , y ), la condition (7) donne les deux relations, appelées conditions de Cauchy-Riemann:
Réciproquement, si f est une fonction dérivable des deux variables x et y satisfaisant à la condition (7), elle est dérivable au sens complexe. Si on pose f (x , y ) = P(x , y ) + i Q(x , y ), la condition (7) donne les deux relations, appelées conditions de Cauchy-Riemann: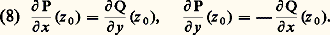 Si f est une fonction dérivable des deux variables réelles x, y, on pose souvent:
Si f est une fonction dérivable des deux variables réelles x, y, on pose souvent: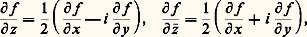 ce qui est suggéré par l’expression de la différentielle:
ce qui est suggéré par l’expression de la différentielle:
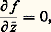 et on a, si f est dérivable au sens complexe:
et on a, si f est dérivable au sens complexe: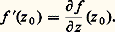 Dans ce qui suit, on va montrer qu’une fonction f est analytique dans un ouvert U si et seulement si elle est continûment dérivable au sens complexe dans U (cela signifie que f est une fonction continue dans U). D’après ce qui précède, cela revient à dire que f (z ) est analytique si et seulement si f (x , y ) est une fonction continûment dérivable des deux variables x , y qui satisfait, en tout point z = x + iy de U, à l’une des conditions équivalentes (7) ou (8).Dérivation des fonctions analytiquesMontrons tout d’abord que toute fonction analytique est indéfiniment dérivable au sens complexe et que sa dérivée est encore une fonction analytique. La dérivabilité et l’analyticité étant des propriétés locales (cela veut dire que si tout point U est centre d’un disque dans lequel ces propriétés sont vraies, alors elles sont vraies dans U), il suffit d’établir le résultat suivant:Théorème 3. Soit:
Dans ce qui suit, on va montrer qu’une fonction f est analytique dans un ouvert U si et seulement si elle est continûment dérivable au sens complexe dans U (cela signifie que f est une fonction continue dans U). D’après ce qui précède, cela revient à dire que f (z ) est analytique si et seulement si f (x , y ) est une fonction continûment dérivable des deux variables x , y qui satisfait, en tout point z = x + iy de U, à l’une des conditions équivalentes (7) ou (8).Dérivation des fonctions analytiquesMontrons tout d’abord que toute fonction analytique est indéfiniment dérivable au sens complexe et que sa dérivée est encore une fonction analytique. La dérivabilité et l’analyticité étant des propriétés locales (cela veut dire que si tout point U est centre d’un disque dans lequel ces propriétés sont vraies, alors elles sont vraies dans U), il suffit d’établir le résultat suivant:Théorème 3. Soit: la somme d’une série entière dans un disque D(a , r ); alors la fonction f est dérivable dans D(a , r ), et on a:
la somme d’une série entière dans un disque D(a , r ); alors la fonction f est dérivable dans D(a , r ), et on a: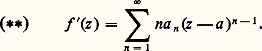 Remarquons tout d’abord que, puisque:
Remarquons tout d’abord que, puisque: la formule d’Hadamard (3) montre que les séries entières () et () ont le même rayon de convergence. Par translation, on se ramène à a = 0.Soit z 0 捻 D(0, r ) et choisissons 福 tel que |z 0| 麗 福 麗 r ; désignons enfin par g (z ) la somme de la série () pour |z | 麗 r . On a, pour z z 0:
la formule d’Hadamard (3) montre que les séries entières () et () ont le même rayon de convergence. Par translation, on se ramène à a = 0.Soit z 0 捻 D(0, r ) et choisissons 福 tel que |z 0| 麗 福 麗 r ; désignons enfin par g (z ) la somme de la série () pour |z | 麗 r . On a, pour z z 0: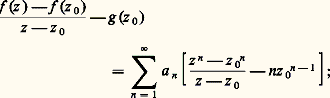
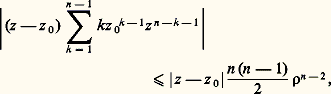 pour |z | 麗 福. Par suite:
pour |z | 麗 福. Par suite: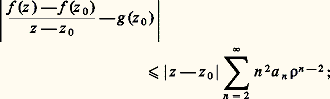 cette dernière série est convergente, puisque 福 麗 r , et f est donc dérivable en z 0, de dérivée f (z 0) = g (z 0).Puisque f est analytique, on peut lui appliquer de nouveau le théorème 3. Par récurrence, on obtient que f est indéfiniment dérivable au sens complexe et que sa dérivée k -ième est:
cette dernière série est convergente, puisque 福 麗 r , et f est donc dérivable en z 0, de dérivée f (z 0) = g (z 0).Puisque f est analytique, on peut lui appliquer de nouveau le théorème 3. Par récurrence, on obtient que f est indéfiniment dérivable au sens complexe et que sa dérivée k -ième est: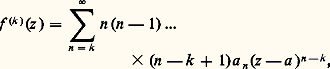
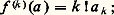 ainsi les coefficients a k du développement () s’expriment simplement en fonction des valeurs des dérivées de f au point a . Si f est une fonction analytique dans un ouvert U, son développement en série entière de centre a est:
ainsi les coefficients a k du développement () s’expriment simplement en fonction des valeurs des dérivées de f au point a . Si f est une fonction analytique dans un ouvert U, son développement en série entière de centre a est: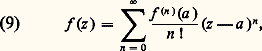 dans un voisinage de tout point a 捻 U; c’est la formule de Taylor de f au point a . Cela redémontre, en particulier, l’unicité de ce développement en série entière de centre a .Il résulte du théorème 3 que, si:
dans un voisinage de tout point a 捻 U; c’est la formule de Taylor de f au point a . Cela redémontre, en particulier, l’unicité de ce développement en série entière de centre a .Il résulte du théorème 3 que, si: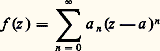
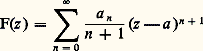 est une fonction analytique dans D(a , r ) qui admet f pour dérivée au sens complexe; on dira que c’est une primitive de f au sens complexe. On a ainsi établi que toute fonction analytique possède localement une primitive définie à une constante additive près, c’est-à-dire que tout point de l’ouvert U dans lequel U est analytique est centre d’un disque dans lequel f admet une primitive. Mais l’existence d’une primitive n’étant pas une notion locale, on ne peut rien obtenir de plus pour l’instant. Il sera nécessaire d’introduire une nouvelle notion, de nature topologique, la simple connexité (cf. infra , L’homotopie , chap. 4), pour aborder globalement le problème des primitives d’une fonction analytique dans un ouvert.Analyticité des fonctions dérivablesOn se propose maintenant de montrer que toute fonction continûment dérivable (au sens complexe) dans un disque de centre a est somme dans ce disque d’une série entière. Avec le théorème 3, cela établira l’équivalence complète entre l’analyticité et la continue dérivabilité au sens complexe dans un ouvert U. Par translation, on se ramène à un disque ouvert de centre O.Théorème 4 . Soit f une fonction continûment dérivable (au sens complexe) pour |z | 麗 R; pour r 麗 R, posons:
est une fonction analytique dans D(a , r ) qui admet f pour dérivée au sens complexe; on dira que c’est une primitive de f au sens complexe. On a ainsi établi que toute fonction analytique possède localement une primitive définie à une constante additive près, c’est-à-dire que tout point de l’ouvert U dans lequel U est analytique est centre d’un disque dans lequel f admet une primitive. Mais l’existence d’une primitive n’étant pas une notion locale, on ne peut rien obtenir de plus pour l’instant. Il sera nécessaire d’introduire une nouvelle notion, de nature topologique, la simple connexité (cf. infra , L’homotopie , chap. 4), pour aborder globalement le problème des primitives d’une fonction analytique dans un ouvert.Analyticité des fonctions dérivablesOn se propose maintenant de montrer que toute fonction continûment dérivable (au sens complexe) dans un disque de centre a est somme dans ce disque d’une série entière. Avec le théorème 3, cela établira l’équivalence complète entre l’analyticité et la continue dérivabilité au sens complexe dans un ouvert U. Par translation, on se ramène à un disque ouvert de centre O.Théorème 4 . Soit f une fonction continûment dérivable (au sens complexe) pour |z | 麗 R; pour r 麗 R, posons:
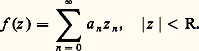
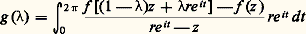 est continue et dérivable pour 0 諒 諒 1 (puisque, pour z fixé, la fonction sous le signe d’intégration est une fonction continûment dérivable de (t ,)), et sa dérivée s’obtient par dérivation par rapport à sous le signe d’intégration. Ainsi:
est continue et dérivable pour 0 諒 諒 1 (puisque, pour z fixé, la fonction sous le signe d’intégration est une fonction continûment dérivable de (t ,)), et sa dérivée s’obtient par dérivation par rapport à sous le signe d’intégration. Ainsi: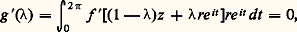
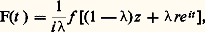 qui est périodique de période 2 神, d’où g () = F(2 神) 漣 F(0) = 0. Ainsi, g est constante dans [0, 1], donc nulle puisque g (0) = 0. Écrivant que g (1) = 0, on obtient, en sortant f (z ):
qui est périodique de période 2 神, d’où g () = F(2 神) 漣 F(0) = 0. Ainsi, g est constante dans [0, 1], donc nulle puisque g (0) = 0. Écrivant que g (1) = 0, on obtient, en sortant f (z ):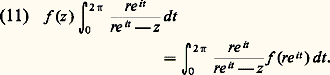
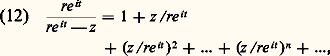 où cette série est normalement convergente pour t réel. On peut donc intégrer terme à terme, ce qui donne:
où cette série est normalement convergente pour t réel. On peut donc intégrer terme à terme, ce qui donne: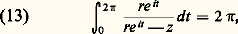 puisque seul le terme constant a une intégrale non nulle. De même, f (re it ) est borné pour t réel; on peut donc intégrer terme à terme son produit avec les deux membres de (12), ce qui donne, d’après (11), en tenant compte de (13):
puisque seul le terme constant a une intégrale non nulle. De même, f (re it ) est borné pour t réel; on peut donc intégrer terme à terme son produit avec les deux membres de (12), ce qui donne, d’après (11), en tenant compte de (13):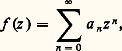 les a n ayant la valeur indiquée par (10). Le fait que les coefficients a n sont indépendants de r résulte de l’unicité du développement en série entière.Donnons une autre conséquence du théorème 4. Si f est analytique dans un ouvert U, pour tout point a 捻 U elle est continûment dérivable dans le plus grand disque ouvert de centre a contenu dans U, donc développable en série entière de centre a dans ce disque; par suite, le rayon de convergence de la série de Taylor de f en a est supérieur ou égal au rayon de ce disque, qui est la distance de a à la frontière de U (cf. chap 7).Indiquons enfin qu’on peut établir le théorème 4 sous l’hypothèse plus faible que f est continue dans D(0, R) et dérivable au sens complexe en tout point, sans supposer la continuité de f (théorème de Goursat); la difficulté est alors de montrer que la fonction g () qui figure dans la démonstration est encore dérivable, de dérivée nulle. Cela entraîne que, si f est dérivable au sens complexe en tout point d’un ouvert U, alors f est analytique dans U (donc indéfiniment dérivable au sens complexe).3. Les coefficients de la série de TaylorLa formule (10) qui donne une expression intégrale des coefficients du développement en série entière va nous donner de précieux renseignements.La propriété de moyenneConsidérons tout d’abord le terme constant de la formule de Taylor. On a, pour n = 0 dans (10):
les a n ayant la valeur indiquée par (10). Le fait que les coefficients a n sont indépendants de r résulte de l’unicité du développement en série entière.Donnons une autre conséquence du théorème 4. Si f est analytique dans un ouvert U, pour tout point a 捻 U elle est continûment dérivable dans le plus grand disque ouvert de centre a contenu dans U, donc développable en série entière de centre a dans ce disque; par suite, le rayon de convergence de la série de Taylor de f en a est supérieur ou égal au rayon de ce disque, qui est la distance de a à la frontière de U (cf. chap 7).Indiquons enfin qu’on peut établir le théorème 4 sous l’hypothèse plus faible que f est continue dans D(0, R) et dérivable au sens complexe en tout point, sans supposer la continuité de f (théorème de Goursat); la difficulté est alors de montrer que la fonction g () qui figure dans la démonstration est encore dérivable, de dérivée nulle. Cela entraîne que, si f est dérivable au sens complexe en tout point d’un ouvert U, alors f est analytique dans U (donc indéfiniment dérivable au sens complexe).3. Les coefficients de la série de TaylorLa formule (10) qui donne une expression intégrale des coefficients du développement en série entière va nous donner de précieux renseignements.La propriété de moyenneConsidérons tout d’abord le terme constant de la formule de Taylor. On a, pour n = 0 dans (10):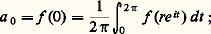 par translation, on aurait, pour tout point a 捻 U:
par translation, on aurait, pour tout point a 捻 U: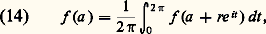 pour tout r assez petit. Cette relation exprime que la valeur de f en a est égale à la valeur moyenne de f sur les cercles de centre a et de rayon r assez petit, ce qu’on exprime en disant que f possède la propriété de moyenne. Il est clair que la partie réelle et la partie imaginaire de f possèdent encore ces propriétés: ce sont des fonctions harmoniques [cf. POTENTIEL ET FONCTIONS HARMONIQUES].Le principe du maximumUne importante conséquence de la propriété de moyenne est le principe du maximum , que l’on peut énoncer ainsi: Soit U un ouvert connexe du plan complexe et f une fonction analytique dans U; s’il existe un point a 捻 U tel que l’on ait |f (z )| 諒 |f (a )| dans tout un disque de centre a (on dit alors que la fonction |f | a un maximum relatif en a ), alors f est constante dans l’ouvert U.Pour cela, remarquons d’abord que, si f (a ) = 0, alors on a f (z ) = 0 dans tout un voisinage de a , d’où f = 0 dans U tout entier. Supposons donc f (a ) 0; multipliant f par une constante complexe, on se ramène au cas où f (a ) est réel positif. D’après le principe du prolongement analytique, il suffit de montrer que f est constante dans un voisinage de a .Soit R tel que |f (z )| 諒 f (a ) pour |z 漣 a | 麗 R, et limitons-nous à des valeurs r 麗 R; soit M(r ) la borne supérieure de f (z ) pour |z | = r . D’après l’hypothèse, on a donc M(r ) 諒 f (a ). De plus, d’après la propriété de moyenne (14), on a f (a ) 諒 M(r ) et, par suite, f (a ) = M(r ). Considérons la fonction u (z ) qui est la partie réelle de f (a ) 漣 f (z ), u (z ) = f (a ) 漣 Ref (z ); on a u (z ) 閭 0, puisque Re f 諒 |f | et u (z ) = 0 si et seulement si f (z ) = f (a ). Or u est la partie réelle d’une fonction holomorphe, donc possède la propriété de moyenne: sa moyenne sur le cercle |z 漣 a | = r est égale à g (a ), donc nulle:
pour tout r assez petit. Cette relation exprime que la valeur de f en a est égale à la valeur moyenne de f sur les cercles de centre a et de rayon r assez petit, ce qu’on exprime en disant que f possède la propriété de moyenne. Il est clair que la partie réelle et la partie imaginaire de f possèdent encore ces propriétés: ce sont des fonctions harmoniques [cf. POTENTIEL ET FONCTIONS HARMONIQUES].Le principe du maximumUne importante conséquence de la propriété de moyenne est le principe du maximum , que l’on peut énoncer ainsi: Soit U un ouvert connexe du plan complexe et f une fonction analytique dans U; s’il existe un point a 捻 U tel que l’on ait |f (z )| 諒 |f (a )| dans tout un disque de centre a (on dit alors que la fonction |f | a un maximum relatif en a ), alors f est constante dans l’ouvert U.Pour cela, remarquons d’abord que, si f (a ) = 0, alors on a f (z ) = 0 dans tout un voisinage de a , d’où f = 0 dans U tout entier. Supposons donc f (a ) 0; multipliant f par une constante complexe, on se ramène au cas où f (a ) est réel positif. D’après le principe du prolongement analytique, il suffit de montrer que f est constante dans un voisinage de a .Soit R tel que |f (z )| 諒 f (a ) pour |z 漣 a | 麗 R, et limitons-nous à des valeurs r 麗 R; soit M(r ) la borne supérieure de f (z ) pour |z | = r . D’après l’hypothèse, on a donc M(r ) 諒 f (a ). De plus, d’après la propriété de moyenne (14), on a f (a ) 諒 M(r ) et, par suite, f (a ) = M(r ). Considérons la fonction u (z ) qui est la partie réelle de f (a ) 漣 f (z ), u (z ) = f (a ) 漣 Ref (z ); on a u (z ) 閭 0, puisque Re f 諒 |f | et u (z ) = 0 si et seulement si f (z ) = f (a ). Or u est la partie réelle d’une fonction holomorphe, donc possède la propriété de moyenne: sa moyenne sur le cercle |z 漣 a | = r est égale à g (a ), donc nulle: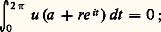 puisque u est continue 閭 0, cela entraîne u (z ) = 0, donc f (z ) = f (a ), dans tout le disque D(a , R).Voici par exemple une conséquence du principe du maximum qui sert souvent. Si f est une fonction analytique dans un disque D(a , R), alors on a, pour r 麗 R:
puisque u est continue 閭 0, cela entraîne u (z ) = 0, donc f (z ) = f (a ), dans tout le disque D(a , R).Voici par exemple une conséquence du principe du maximum qui sert souvent. Si f est une fonction analytique dans un disque D(a , R), alors on a, pour r 麗 R: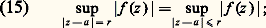 en effet, la fonction continue |f | atteint sa borne supérieure dans D(0, r ) en un point qui, d’après le principe du maximum, est nécessairement un point frontière, sinon f serait constante (et alors (15) trivial). Ce raisonnement s’appliquerait à tout compact (ensemble fermé et borné) du plan: si f est analytique dans un ouvert connexe D d’adhérence D 漣 compacte et continue sur D 漣, alors |f | n’atteint son maximum qu’en un point frontière, sinon elle est constante. Donnons une application de (15) en établissant le lemme de Schwarz , qui sert dans la théorie de la représentation conforme (cf. FONCTIONS ANALYTIQUES – Représentation conforme): Soit f une fonction analytique pour |z | 麗 1 telle que f (0) = 0 et |f (z )| 麗 1 pour |z | 麗 1; alors on a |f (z )| 諒 |z | pour |z | 麗 1, avec égalité en un point z 0 0, si et seulement si f (z ) =z , constante complexe du module 1.En effet, on a:
en effet, la fonction continue |f | atteint sa borne supérieure dans D(0, r ) en un point qui, d’après le principe du maximum, est nécessairement un point frontière, sinon f serait constante (et alors (15) trivial). Ce raisonnement s’appliquerait à tout compact (ensemble fermé et borné) du plan: si f est analytique dans un ouvert connexe D d’adhérence D 漣 compacte et continue sur D 漣, alors |f | n’atteint son maximum qu’en un point frontière, sinon elle est constante. Donnons une application de (15) en établissant le lemme de Schwarz , qui sert dans la théorie de la représentation conforme (cf. FONCTIONS ANALYTIQUES – Représentation conforme): Soit f une fonction analytique pour |z | 麗 1 telle que f (0) = 0 et |f (z )| 麗 1 pour |z | 麗 1; alors on a |f (z )| 諒 |z | pour |z | 麗 1, avec égalité en un point z 0 0, si et seulement si f (z ) =z , constante complexe du module 1.En effet, on a: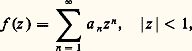 et, par suite, la fonction:
et, par suite, la fonction: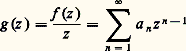 est analytique pour |z | 麗 1. Puisque |f (z )| 麗 1, on a donc |g (z )| 諒 1/r pour |z | = r , et aussi pour |z | 諒 r , d’après (15). Ainsi, fixant z 捻 D(0, 1), on a |f (z )| 諒 |z |/r quel que soit r 礪 |z |, r 麗 1; faisant tendre r vers 1, on a bien |f (z )| 諒 |z |. Si maintenant on a |f (z 0)| = |z 0| pour un point z 0 0, alors la fonction g atteint son maximum en un point du disque D(0, 1); la fonction g est donc constante et on a f (z )/z =, || = 1.Les inégalités de CauchySoit f une fonction analytique dans un disque D(0, R); la fonction f (z ) est donc somme dans D(0, R) d’une série entière dont les coefficients a n sont donnés par la formule (10). Si on désigne par M(r ) le maximum de f (z ) pour |z | = r (c’est aussi, d’après (15), le maximum pour |z | 諒 r ), on obtient donc:
est analytique pour |z | 麗 1. Puisque |f (z )| 麗 1, on a donc |g (z )| 諒 1/r pour |z | = r , et aussi pour |z | 諒 r , d’après (15). Ainsi, fixant z 捻 D(0, 1), on a |f (z )| 諒 |z |/r quel que soit r 礪 |z |, r 麗 1; faisant tendre r vers 1, on a bien |f (z )| 諒 |z |. Si maintenant on a |f (z 0)| = |z 0| pour un point z 0 0, alors la fonction g atteint son maximum en un point du disque D(0, 1); la fonction g est donc constante et on a f (z )/z =, || = 1.Les inégalités de CauchySoit f une fonction analytique dans un disque D(0, R); la fonction f (z ) est donc somme dans D(0, R) d’une série entière dont les coefficients a n sont donnés par la formule (10). Si on désigne par M(r ) le maximum de f (z ) pour |z | = r (c’est aussi, d’après (15), le maximum pour |z | 諒 r ), on obtient donc: Comme conséquence simple de (16), on obtient le théorème de Liouville : Une fonction analytique dans tout le plan et bornée est constante. En effet, cette fonction est alors développable en série de rayon de convergence infini; les inégalités (16) entraînent que les coefficients a n de ce développement vérifient:
Comme conséquence simple de (16), on obtient le théorème de Liouville : Une fonction analytique dans tout le plan et bornée est constante. En effet, cette fonction est alors développable en série de rayon de convergence infini; les inégalités (16) entraînent que les coefficients a n de ce développement vérifient: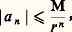 quel que soit r . Pour r tendant vers l’infini, on obtient a n = 0 pour n 閭 1. Le théorème de Liouville fournit une démonstration extrêmement simple du «théorème fondamental de l’algèbre», le théorème de d’Alembert : Tout polynôme à coefficients complexes de degré 閭 1 a au moins une racine complexe. En effet, soit:
quel que soit r . Pour r tendant vers l’infini, on obtient a n = 0 pour n 閭 1. Le théorème de Liouville fournit une démonstration extrêmement simple du «théorème fondamental de l’algèbre», le théorème de d’Alembert : Tout polynôme à coefficients complexes de degré 閭 1 a au moins une racine complexe. En effet, soit: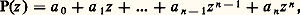 où a n 0, n 閭 1, un tel polynôme; raisonnons par l’absurde, en supposant P(z ) 0 pour tout z 捻 C. La fonction 1/P(z ) est alors analytique dans tout le plan et bornée, car |P(z )|秊 pour |z |秊; le théorème de Liouville entraîne alors que cette fonction est constante, en contradiction avec l’hypothèse.4. Le problème des primitivesNous avons obtenu maintenant à peu près tous les résultats qu’il est possible de démontrer localement , c’est-à-dire à partir de l’étude des séries entières; pour continuer la théorie, nous avons besoin d’un remarquable outil introduit par Cauchy, l’intégrale curviligne le long d’une courbe.L’intégrale curviligneOn va tout d’abord préciser la terminologie et les conditions de régularité auxquelles seront soumises les «courbes» du plan qui interviennent dans la suite.On appelle chemin dans le plan complexe toute application continue 塚: IC d’un intervalle I = [a , b ] dans le plan complexe qui est continûment dérivable par morceaux; cela signifie que I est une réunion d’un nombre fini d’intervalles fermés dans lesquels 塚 est continûment dérivable, ou encore que 塚 est la primitive d’une fonction continue par morceaux dans I. Le point 塚(a ) s’appelle l’origine du chemin 塚 et le point 塚(b ) est son extrémité ; un chemin fermé, c’est-à-dire tel que 塚(a ) = 塚(b ) sera appelé un lacet . Enfin, on appelle trajectoire le sous-ensemble 塚(I) du plan complexe parcouru par 塚(t ) pour t 捻 I; si 塚 est un chemin, on le représentera géométriquement en dessinant sa trajectoire et en indiquant par des flèches le «sens de parcours» du point 塚(t ) lorsque t croît de a à b . L’exemple le plus simple d’une telle situation est celui d’une fonction affine par morceaux: la trajectoire est alors une ligne brisée (cf. chap. 1). Soit maintenant n un entier relatif non nul, z 0 un nombre complexe et r un nombre réel positif; pour t 捻 [0, 2 神], l’application:
où a n 0, n 閭 1, un tel polynôme; raisonnons par l’absurde, en supposant P(z ) 0 pour tout z 捻 C. La fonction 1/P(z ) est alors analytique dans tout le plan et bornée, car |P(z )|秊 pour |z |秊; le théorème de Liouville entraîne alors que cette fonction est constante, en contradiction avec l’hypothèse.4. Le problème des primitivesNous avons obtenu maintenant à peu près tous les résultats qu’il est possible de démontrer localement , c’est-à-dire à partir de l’étude des séries entières; pour continuer la théorie, nous avons besoin d’un remarquable outil introduit par Cauchy, l’intégrale curviligne le long d’une courbe.L’intégrale curviligneOn va tout d’abord préciser la terminologie et les conditions de régularité auxquelles seront soumises les «courbes» du plan qui interviennent dans la suite.On appelle chemin dans le plan complexe toute application continue 塚: IC d’un intervalle I = [a , b ] dans le plan complexe qui est continûment dérivable par morceaux; cela signifie que I est une réunion d’un nombre fini d’intervalles fermés dans lesquels 塚 est continûment dérivable, ou encore que 塚 est la primitive d’une fonction continue par morceaux dans I. Le point 塚(a ) s’appelle l’origine du chemin 塚 et le point 塚(b ) est son extrémité ; un chemin fermé, c’est-à-dire tel que 塚(a ) = 塚(b ) sera appelé un lacet . Enfin, on appelle trajectoire le sous-ensemble 塚(I) du plan complexe parcouru par 塚(t ) pour t 捻 I; si 塚 est un chemin, on le représentera géométriquement en dessinant sa trajectoire et en indiquant par des flèches le «sens de parcours» du point 塚(t ) lorsque t croît de a à b . L’exemple le plus simple d’une telle situation est celui d’une fonction affine par morceaux: la trajectoire est alors une ligne brisée (cf. chap. 1). Soit maintenant n un entier relatif non nul, z 0 un nombre complexe et r un nombre réel positif; pour t 捻 [0, 2 神], l’application: est un lacet dont la trajectoire est le cercle de centre z 0 et de rayon r [cf. EXPONENTIELLE ET LOGARITHME]. Nous dirons que ce lacet est ce cercle «parcouru n fois», car tout point de ce cercle est l’image de |n | valeurs distinctes de t 捻 [0, 2 神]; on dira aussi que c’est ce cercle parcouru une fois dans le sens direct si n = 1 et dans le sens rétrograde si n = 漣 1.Pour l’intégrale curviligne, nous aurons besoin d’une notion de courbe orientée plus «géométriquement», c’est-à-dire indépendante dans une certaine mesure du paramétrage 塚. Nous dirons que deux chemins:
est un lacet dont la trajectoire est le cercle de centre z 0 et de rayon r [cf. EXPONENTIELLE ET LOGARITHME]. Nous dirons que ce lacet est ce cercle «parcouru n fois», car tout point de ce cercle est l’image de |n | valeurs distinctes de t 捻 [0, 2 神]; on dira aussi que c’est ce cercle parcouru une fois dans le sens direct si n = 1 et dans le sens rétrograde si n = 漣 1.Pour l’intégrale curviligne, nous aurons besoin d’une notion de courbe orientée plus «géométriquement», c’est-à-dire indépendante dans une certaine mesure du paramétrage 塚. Nous dirons que deux chemins: sont équivalents s’il existe une bijection continue 﨏 croissante de I1 sur I2, continûment dérivable par morceaux ainsi que la bijection réciproque, telle que 塚1(t ) = 塚2( 﨏(t )) pour tout t 捻 I1. Par exemple, pour tout chemin, on peut trouver, par une homothétie suivie d’une translation, un chemin équivalent défini dans un intervalle fixe de R, par exemple [0, 1].Soit maintenant 塚: [a , b ]C un chemin et f une fonction à valeurs complexes définie et continue sur la trajectoire de 塚. D’après les conditions de régularité imposées à 塚, la fonction t 料 f ( 塚(t )) 塚 (t ) est continue par morceaux, donc intégrable, dans [a , b ]. On appelle intégrale curviligne le long du chemin 塚 le nombre complexe:
sont équivalents s’il existe une bijection continue 﨏 croissante de I1 sur I2, continûment dérivable par morceaux ainsi que la bijection réciproque, telle que 塚1(t ) = 塚2( 﨏(t )) pour tout t 捻 I1. Par exemple, pour tout chemin, on peut trouver, par une homothétie suivie d’une translation, un chemin équivalent défini dans un intervalle fixe de R, par exemple [0, 1].Soit maintenant 塚: [a , b ]C un chemin et f une fonction à valeurs complexes définie et continue sur la trajectoire de 塚. D’après les conditions de régularité imposées à 塚, la fonction t 料 f ( 塚(t )) 塚 (t ) est continue par morceaux, donc intégrable, dans [a , b ]. On appelle intégrale curviligne le long du chemin 塚 le nombre complexe: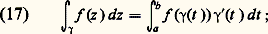 par exemple, si 塚 est le cercle de centre z 0 et de rayon r parcouru une fois dans le sens direct (cf. supra ) et f une fonction continue sur ce cercle, on a:
par exemple, si 塚 est le cercle de centre z 0 et de rayon r parcouru une fois dans le sens direct (cf. supra ) et f une fonction continue sur ce cercle, on a: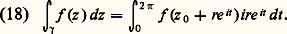 La notion d’équivalence des chemins introduite ci-dessus s’avère particulièrement bien adaptée à l’intégrale curviligne; en effet, la formule de changement de variable dans une intégrale montre que, si 塚1 et 塚2 sont des chemins équivalents et f une fonction continue sur leur trajectoire commune, les intégrales curvilignes de f sur 塚1 et sur 塚2 sont égales.Indiquons enfin comment on peut majorer une intégrale curviligne: si |f (z )| 諒 M pour tout point z de la trajectoire de 塚, on a:
La notion d’équivalence des chemins introduite ci-dessus s’avère particulièrement bien adaptée à l’intégrale curviligne; en effet, la formule de changement de variable dans une intégrale montre que, si 塚1 et 塚2 sont des chemins équivalents et f une fonction continue sur leur trajectoire commune, les intégrales curvilignes de f sur 塚1 et sur 塚2 sont égales.Indiquons enfin comment on peut majorer une intégrale curviligne: si |f (z )| 諒 M pour tout point z de la trajectoire de 塚, on a: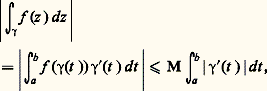 et cette dernière intégrale n’est autre que la longueur L( 塚) du chemin [cf. GÉOMÉTRIE DIFFÉRENTIELLE CLASSIQUE]. Ainsi:
et cette dernière intégrale n’est autre que la longueur L( 塚) du chemin [cf. GÉOMÉTRIE DIFFÉRENTIELLE CLASSIQUE]. Ainsi: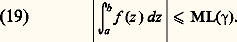 Lien avec les primitivesSi la fonction f est définie dans un ouvert U contenant la trajectoire de 塚 et est dans cet ouvert la dérivée au sens complexe d’une fonction continue F (d’après ce qui précède, F est alors nécessairement analytique), alors:
Lien avec les primitivesSi la fonction f est définie dans un ouvert U contenant la trajectoire de 塚 et est dans cet ouvert la dérivée au sens complexe d’une fonction continue F (d’après ce qui précède, F est alors nécessairement analytique), alors: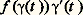 est, sauf pour un nombre fini de valeurs de t , la dérivée de la fonction continue F( 塚(t )); par suite:
est, sauf pour un nombre fini de valeurs de t , la dérivée de la fonction continue F( 塚(t )); par suite: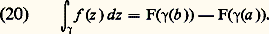 En particulier, si une fonction f analytique dans un ouvert U admet une primitive (au sens complexe) dans cet ouvert, alors l’intégrale curviligne de f le long de tout lacet est nulle. Il est remarquable que, comme nous allons le montrer maintenant, cette condition est caractéristique: une fonction f analytique dans un ouvert connexe U admet une primitive dans U si et seulement si:
En particulier, si une fonction f analytique dans un ouvert U admet une primitive (au sens complexe) dans cet ouvert, alors l’intégrale curviligne de f le long de tout lacet est nulle. Il est remarquable que, comme nous allons le montrer maintenant, cette condition est caractéristique: une fonction f analytique dans un ouvert connexe U admet une primitive dans U si et seulement si: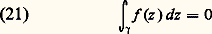 pour tout lacet 塚 dont la trajectoire est contenue dans U.Pour cela, remarquons tout d’abord que l’hypothèse (21) entraîne que, si 塚1 et 塚2 sont deux chemins de U de même origine et de même extrémité , alors les intégrales curvilignes de f le long de 塚1 et de 塚2 sont égales . En effet, si nous désignons par 塚20 le chemin «opposé» à 塚2, c’est-à-dire le chemin 塚2 «parcouru en sens inverse» (défini mathématiquement par:
pour tout lacet 塚 dont la trajectoire est contenue dans U.Pour cela, remarquons tout d’abord que l’hypothèse (21) entraîne que, si 塚1 et 塚2 sont deux chemins de U de même origine et de même extrémité , alors les intégrales curvilignes de f le long de 塚1 et de 塚2 sont égales . En effet, si nous désignons par 塚20 le chemin «opposé» à 塚2, c’est-à-dire le chemin 塚2 «parcouru en sens inverse» (défini mathématiquement par: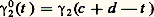 si 塚2: [c , d ]C), l’intégrale de la fonction f le long de 塚20 est l’opposée de l’intégrale de f le long de 塚2. Le chemin obtenu par juxtaposition de 塚1 et de 塚20, en parcourant «successivement» 塚1, puis 塚20, est alors un lacet ; d’où, d’après (21):
si 塚2: [c , d ]C), l’intégrale de la fonction f le long de 塚20 est l’opposée de l’intégrale de f le long de 塚2. Le chemin obtenu par juxtaposition de 塚1 et de 塚20, en parcourant «successivement» 塚1, puis 塚20, est alors un lacet ; d’où, d’après (21):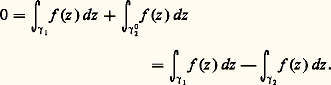 Pour f analytique dans U connexe satisfaisant à la condition (21), fixons un point a 捻 U; d’après ce qui précède, la valeur F(z ) de l’intégrale curviligne de f le long d’un chemin 塚(z ) de U d’origine a et d’extrémité z est indépendante du choix de ce chemin (il existe au moins un tel chemin qui soit une ligne brisée, cf. supra , chap. 1, Principe des zéros isolés , car U est connexe). Montrons que F est une fonction analytique qui a pour dérivée f dans U; soit z 0 un point de U. Il existe un disque D(z 0, 見) dans lequel f est développable en série entière. Pour tout point z de ce disque, F(z ) est l’intégrale curviligne de f le long de tout chemin de U d’origine a et d’extrémité z , par exemple le chemin obtenu en parcourant successivement un chemin 塚(z 0) d’origine a et d’extrémité z 0; d’où une intégrale curviligne égale à F(z 0), puis le segment [z 0, z ], soit:
Pour f analytique dans U connexe satisfaisant à la condition (21), fixons un point a 捻 U; d’après ce qui précède, la valeur F(z ) de l’intégrale curviligne de f le long d’un chemin 塚(z ) de U d’origine a et d’extrémité z est indépendante du choix de ce chemin (il existe au moins un tel chemin qui soit une ligne brisée, cf. supra , chap. 1, Principe des zéros isolés , car U est connexe). Montrons que F est une fonction analytique qui a pour dérivée f dans U; soit z 0 un point de U. Il existe un disque D(z 0, 見) dans lequel f est développable en série entière. Pour tout point z de ce disque, F(z ) est l’intégrale curviligne de f le long de tout chemin de U d’origine a et d’extrémité z , par exemple le chemin obtenu en parcourant successivement un chemin 塚(z 0) d’origine a et d’extrémité z 0; d’où une intégrale curviligne égale à F(z 0), puis le segment [z 0, z ], soit: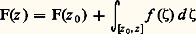
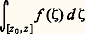 est une primitive de f dans ce disque.Remarquons que la condition (21) n’est pas toujours satisfaite. Par exemple la fonction f (z ) = 1/z est analytique dans l’ouvert connexe C complémentaire de O dans le plan complexe, et son intégrale le long du cercle |z | = 1 parcouru une fois dans le sens direct est:
est une primitive de f dans ce disque.Remarquons que la condition (21) n’est pas toujours satisfaite. Par exemple la fonction f (z ) = 1/z est analytique dans l’ouvert connexe C complémentaire de O dans le plan complexe, et son intégrale le long du cercle |z | = 1 parcouru une fois dans le sens direct est: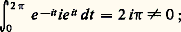 ainsi, cette fonction n’admet pas de primitive dans C.On voit ainsi que la recherche d’une primitive d’une fonction analytique dans un ouvert U est un problème qui n’a pas toujours de solution. Pour aborder cette question nous aurons besoin d’introduire de nouvelles notions de topologie du plan. En particulier, on va voir que, si U satisfait à une condition de nature géométrique: être «simplement connexe» (cf. infra , Théorème de Cauchy ), alors toute fonction analytique dans U a une primitive dans U.L’homotopieSoit U un ouvert du plan complexe et 塚1 et 塚2 deux lacets de U; quitte à remplacer l’un d’entre eux par un lacet équivalent, on peut supposer qu’ils sont définis dans le même intervalle I = [a , b ] de R. On dit que ces deux lacets sont homotopes dans U s’il existe une application continue :
ainsi, cette fonction n’admet pas de primitive dans C.On voit ainsi que la recherche d’une primitive d’une fonction analytique dans un ouvert U est un problème qui n’a pas toujours de solution. Pour aborder cette question nous aurons besoin d’introduire de nouvelles notions de topologie du plan. En particulier, on va voir que, si U satisfait à une condition de nature géométrique: être «simplement connexe» (cf. infra , Théorème de Cauchy ), alors toute fonction analytique dans U a une primitive dans U.L’homotopieSoit U un ouvert du plan complexe et 塚1 et 塚2 deux lacets de U; quitte à remplacer l’un d’entre eux par un lacet équivalent, on peut supposer qu’ils sont définis dans le même intervalle I = [a , b ] de R. On dit que ces deux lacets sont homotopes dans U s’il existe une application continue :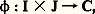 J = [c , d ] 說 R, telle que 﨏(t , c ) = 塚1(t ), 﨏(t , d ) = 塚2(t ) pour tout t 捻 I, et 﨏(a , u ) = 﨏(b , u ) pour tout u 捻 J; intuitivement, cela signifie qu’on peut «passer» de 塚1 à 塚2, sans sortir de U, par une «famille continue» de courbes fermées Cu (de représentation paramétrique t 料 﨏(t , u )).Cette notion d’homotopie des lacets est fondamentale dans toute la théorie de Cauchy; on définit ainsi une relation d’équivalence sur l’ensemble des classes de lacets équivalents (au sens ci-dessus).L’homotopie va permettre d’introduire une importante notion géométrique. On dit qu’un ouvert U du plan est simplement connexe si tout lacet de U est homotope dans U à un lacet constant, de trajectoire réduite à un point. Un exemple important est constitué par les ouverts étoilés par rapport à un point ; cela signifie qu’il existe un point a d’un tel ouvert U tel que le segment [a , z ] soit entièrement contenu dans U pour tout z 捻 U. C’est ainsi le cas du complémentaire dans le plan complexe d’une demi-droite fermée, si on prend pour a un point quelconque de la demi-droite opposée. Avec les notations précédentes, si U est un ouvert étoilé par rapport à a et si 塚: IU est un lacet de U, l’application:
J = [c , d ] 說 R, telle que 﨏(t , c ) = 塚1(t ), 﨏(t , d ) = 塚2(t ) pour tout t 捻 I, et 﨏(a , u ) = 﨏(b , u ) pour tout u 捻 J; intuitivement, cela signifie qu’on peut «passer» de 塚1 à 塚2, sans sortir de U, par une «famille continue» de courbes fermées Cu (de représentation paramétrique t 料 﨏(t , u )).Cette notion d’homotopie des lacets est fondamentale dans toute la théorie de Cauchy; on définit ainsi une relation d’équivalence sur l’ensemble des classes de lacets équivalents (au sens ci-dessus).L’homotopie va permettre d’introduire une importante notion géométrique. On dit qu’un ouvert U du plan est simplement connexe si tout lacet de U est homotope dans U à un lacet constant, de trajectoire réduite à un point. Un exemple important est constitué par les ouverts étoilés par rapport à un point ; cela signifie qu’il existe un point a d’un tel ouvert U tel que le segment [a , z ] soit entièrement contenu dans U pour tout z 捻 U. C’est ainsi le cas du complémentaire dans le plan complexe d’une demi-droite fermée, si on prend pour a un point quelconque de la demi-droite opposée. Avec les notations précédentes, si U est un ouvert étoilé par rapport à a et si 塚: IU est un lacet de U, l’application: définie par:
définie par: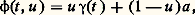 réalise l’homotopie de 塚 sur le lacet constant réduit au point a , car 﨏(t , 0) = 塚(t ), 﨏(t , 1) = a ; on peut écrire:
réalise l’homotopie de 塚 sur le lacet constant réduit au point a , car 﨏(t , 0) = 塚(t ), 﨏(t , 1) = a ; on peut écrire: ce qui montre que 﨏(t , u ) est homothétique de 塚(t ) dans l’homothétie de centre a et de rapport u .Le théorème de CauchyCe résultat exprime que, si f est une fonction analytique dans un ouvert U, la valeur de l’intégrale curviligne de f sur tout lacet de U ne dépend que de la classe d’homotopie de ce lacet dans U. En fait, on peut même montrer, ce qui est plus fort, qu’elle ne dépend que de la classe d’homologie (cf. infra , chap. 5, L’indice ) de ce lacet. D’après ce qui précède, ce résultat est intimement lié au problème de la recherche de primitives «globales» pour une fonction analytique.Théorème de Cauchy . Soit U un ouvert du plan complexe et f une fonction analytique dans U; si 塚1 et 塚2 sont des lacets de U qui sont homotopes dans U, alors:
ce qui montre que 﨏(t , u ) est homothétique de 塚(t ) dans l’homothétie de centre a et de rapport u .Le théorème de CauchyCe résultat exprime que, si f est une fonction analytique dans un ouvert U, la valeur de l’intégrale curviligne de f sur tout lacet de U ne dépend que de la classe d’homotopie de ce lacet dans U. En fait, on peut même montrer, ce qui est plus fort, qu’elle ne dépend que de la classe d’homologie (cf. infra , chap. 5, L’indice ) de ce lacet. D’après ce qui précède, ce résultat est intimement lié au problème de la recherche de primitives «globales» pour une fonction analytique.Théorème de Cauchy . Soit U un ouvert du plan complexe et f une fonction analytique dans U; si 塚1 et 塚2 sont des lacets de U qui sont homotopes dans U, alors: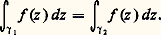 En particulier, si U est simplement connexe, on a:
En particulier, si U est simplement connexe, on a: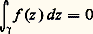 pour tout lacet 塚 de U; par suite, toute fonction analytique dans un ouvert connexe et simplement connexe admet une primitive (au sens complexe) dans cet ouvert.Indiquons, sans entrer dans tous les détails, les grandes lignes d’une démonstration de ce théorème. Soit, avec les notations ci-dessus:
pour tout lacet 塚 de U; par suite, toute fonction analytique dans un ouvert connexe et simplement connexe admet une primitive (au sens complexe) dans cet ouvert.Indiquons, sans entrer dans tous les détails, les grandes lignes d’une démonstration de ce théorème. Soit, avec les notations ci-dessus: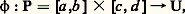 la fonction continue qui réalise l’homotopie. L’ensemble L = 﨏(P) parcouru par 﨏(t , u ) pour (t , u ) 捻 P est compact et inclus dans U (fig. 3; L est ombré). La compacité de L entraîne d’abord qu’il existe 見 礪 0 tel que, pour tout point z 0 捻 L, la fonction f soit développable en série entière en (z 漣 z 0) dans le disque D(z 0, 見) et, par suite (cf. supra , chap. 2, Dérivation des fonctions analytiques ), admette une primitive dans ce disque. D’après la continuité uniforme de 﨏 sur P, il existe alors 﨎 礪 0 tel que |t 漣 t | 麗 﨎 et |u 漣 u | 麗 﨎 entraînent | 﨏(t , u ) 漣 﨏(t , u )| 麗 見/4. Soit maintenant:
la fonction continue qui réalise l’homotopie. L’ensemble L = 﨏(P) parcouru par 﨏(t , u ) pour (t , u ) 捻 P est compact et inclus dans U (fig. 3; L est ombré). La compacité de L entraîne d’abord qu’il existe 見 礪 0 tel que, pour tout point z 0 捻 L, la fonction f soit développable en série entière en (z 漣 z 0) dans le disque D(z 0, 見) et, par suite (cf. supra , chap. 2, Dérivation des fonctions analytiques ), admette une primitive dans ce disque. D’après la continuité uniforme de 﨏 sur P, il existe alors 﨎 礪 0 tel que |t 漣 t | 麗 﨎 et |u 漣 u | 麗 﨎 entraînent | 﨏(t , u ) 漣 﨏(t , u )| 麗 見/4. Soit maintenant: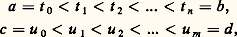 des subdivisions de [a , b ] et [c , d ] respectivement telles que t i+1 漣 t i 麗 﨎 et u j+1 漣 u j 麗 﨎. Posons z i, j = 﨏(t i , u j ) et désignons par 臨j la ligne brisée (fermée) joignant les points z i, j pour i croissant de 0 à n (fig. 3); cette ligne brisée peut être paramétrée par une fonction affine par morceaux et nous désignerons encore par 臨j le lacet ainsi défini.Soit Ai, j l’intégrale curviligne de f le long du segment [z i, j , z i+1, j ] et Bi, j l’intégrale curviligne de f le long du segment [z i, j , z i, j+1 ] (fig. 3). D’après le choix de 﨎 et de la subdivision, les quatre segments correspondant aux intégrales Ai, j , Ai, j+1 , Bi, j , Bi+1, j , sont dans un même disque où il existe une primitive F de f ; on a donc:
des subdivisions de [a , b ] et [c , d ] respectivement telles que t i+1 漣 t i 麗 﨎 et u j+1 漣 u j 麗 﨎. Posons z i, j = 﨏(t i , u j ) et désignons par 臨j la ligne brisée (fermée) joignant les points z i, j pour i croissant de 0 à n (fig. 3); cette ligne brisée peut être paramétrée par une fonction affine par morceaux et nous désignerons encore par 臨j le lacet ainsi défini.Soit Ai, j l’intégrale curviligne de f le long du segment [z i, j , z i+1, j ] et Bi, j l’intégrale curviligne de f le long du segment [z i, j , z i, j+1 ] (fig. 3). D’après le choix de 﨎 et de la subdivision, les quatre segments correspondant aux intégrales Ai, j , Ai, j+1 , Bi, j , Bi+1, j , sont dans un même disque où il existe une primitive F de f ; on a donc: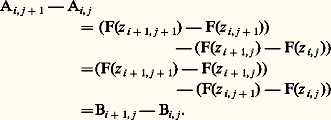 Additionnant les égalités ci-dessus pour i = 0, 1, ..., n 漣 1, on fait disparaître les Bi, j et on obtient:
Additionnant les égalités ci-dessus pour i = 0, 1, ..., n 漣 1, on fait disparaître les Bi, j et on obtient: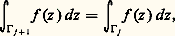 puisqu’il est clair que:
puisqu’il est clair que: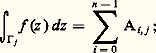 un raisonnement très analogue montrerait que:
un raisonnement très analogue montrerait que: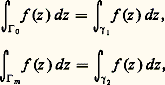 d’où le résultat cherché.Le logarithme complexeIl résulte de ce qui précède que toute fonction analytique dans un domaine simplement connexe admet des primitives dans cet ouvert; de plus, deux telles primitives diffèrent d’une constante au voisinage de chaque point (unicité du développement en série entière) et, par suite, dans l’ouvert connexe tout entier d’après le principe du prolongement analytique (cf. chap. 1, Principe des zéros isolés ). Ainsi, le choix de sa valeur en un point détermine entièrement cette primitive.Voici une importante application de ce résultat. Si f est une fonction analytique dans un domaine simplement connexe U et ne s’annule pas dans U, la fonction f /f est dérivable, donc analytique, dans U et, par suite, admet des primitives dans U. Soit L l’une d’entre elles, telle que l’on ait:
d’où le résultat cherché.Le logarithme complexeIl résulte de ce qui précède que toute fonction analytique dans un domaine simplement connexe admet des primitives dans cet ouvert; de plus, deux telles primitives diffèrent d’une constante au voisinage de chaque point (unicité du développement en série entière) et, par suite, dans l’ouvert connexe tout entier d’après le principe du prolongement analytique (cf. chap. 1, Principe des zéros isolés ). Ainsi, le choix de sa valeur en un point détermine entièrement cette primitive.Voici une importante application de ce résultat. Si f est une fonction analytique dans un domaine simplement connexe U et ne s’annule pas dans U, la fonction f /f est dérivable, donc analytique, dans U et, par suite, admet des primitives dans U. Soit L l’une d’entre elles, telle que l’on ait: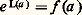 en un point a 捻 U; c’est toujours possible, car f (a ) 0 et tout nombre complexe non nul peut se mettre sous la forme e b , b 捻 C (cf. EXPONENTIELLE ET LOGARITHME, chap. 4). La fonction analytique:
en un point a 捻 U; c’est toujours possible, car f (a ) 0 et tout nombre complexe non nul peut se mettre sous la forme e b , b 捻 C (cf. EXPONENTIELLE ET LOGARITHME, chap. 4). La fonction analytique: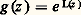 a pour dérivée:
a pour dérivée: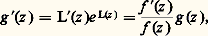 par définition de L. Ainsi:
par définition de L. Ainsi: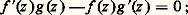
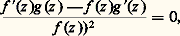 ce qui exprime que la dérivée de la fonction f /g est nulle dans U, et, par suite, que cette fonction est constante dans le domaine simplement connexe U. Cette constante est égale à 1, puisque f (a ) = g (a ), et on a donc:
ce qui exprime que la dérivée de la fonction f /g est nulle dans U, et, par suite, que cette fonction est constante dans le domaine simplement connexe U. Cette constante est égale à 1, puisque f (a ) = g (a ), et on a donc: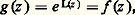 pour tout z 捻 U. On dit que la fonction analytique L est une détermination analytique (en particulier continue) du logarithme de la fonction f .Notamment, il existe des déterminations analytiques du logarithme de z dans tout domaine simplement connexe ne contenant pas O (par exemple, dans le complémentaire d’une demi-droite fermée issue de O); et deux quelconques de ces déterminations diffèrent d’un multiple entier de 2 神i , mais on a vu plus haut qu’il n’existait pas de primitive de 1/z dans le plan complexe privé de O tout entier. Si L est une détermination du logarithme, sa partie imaginaire est une fonction continue qui est égale, en chaque point z , à une des valeurs possibles de l’argument de z . On dit que c’est une détermination continue de l’argument; l’existence, dans un ouvert, d’une détermination continue arg z de l’argument équivaut à l’existence d’une détermination analytique du logarithme, par la formule:
pour tout z 捻 U. On dit que la fonction analytique L est une détermination analytique (en particulier continue) du logarithme de la fonction f .Notamment, il existe des déterminations analytiques du logarithme de z dans tout domaine simplement connexe ne contenant pas O (par exemple, dans le complémentaire d’une demi-droite fermée issue de O); et deux quelconques de ces déterminations diffèrent d’un multiple entier de 2 神i , mais on a vu plus haut qu’il n’existait pas de primitive de 1/z dans le plan complexe privé de O tout entier. Si L est une détermination du logarithme, sa partie imaginaire est une fonction continue qui est égale, en chaque point z , à une des valeurs possibles de l’argument de z . On dit que c’est une détermination continue de l’argument; l’existence, dans un ouvert, d’une détermination continue arg z de l’argument équivaut à l’existence d’une détermination analytique du logarithme, par la formule: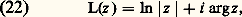 où ln |z | est le logarithme du nombre réel positif |z |. On appelle détermination principale du logarithme de z la détermination analytique du logarithme, définie pour x non réel 諒 0, qui prend la valeur 0 pour z = 1; la détermination correspondante de l’argument prend ses valeurs entre 漣 神 et + 神 et la détermination principale réalise une bijection du plan complexe privé du demi-axe réel négatif sur la «bande» formée des nombres complexes Z = X + i Y tels que 漣 神 麗 Y 麗 + 神 (cf. EXPONENTIELLE ET LOGARITHME, chap. 4). Pour z réel positif, L(z ) est le logarithme de z au sens usuel, et la série de Taylor de cette fonction au point 1 est:
où ln |z | est le logarithme du nombre réel positif |z |. On appelle détermination principale du logarithme de z la détermination analytique du logarithme, définie pour x non réel 諒 0, qui prend la valeur 0 pour z = 1; la détermination correspondante de l’argument prend ses valeurs entre 漣 神 et + 神 et la détermination principale réalise une bijection du plan complexe privé du demi-axe réel négatif sur la «bande» formée des nombres complexes Z = X + i Y tels que 漣 神 麗 Y 麗 + 神 (cf. EXPONENTIELLE ET LOGARITHME, chap. 4). Pour z réel positif, L(z ) est le logarithme de z au sens usuel, et la série de Taylor de cette fonction au point 1 est: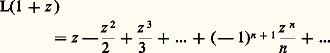 Le théorème de MoreraLe théorème de Cauchy admet une réciproque, qui ne fait intervenir que des intégrales curvilignes le long de contours fermés très simples: le théorème de Morera affirme qu’une fonction f continue dans un ouvert U est analytique dans U si et seulement si son intégrale curviligne le long de tout rectangle, de côtés parallèles aux axes Ox et Oy , assez petit pour être entièrement contenu dans U est nulle. La condition nécessaire résulte du théorème de Cauchy; indiquons le principe de la démonstration de la réciproque. Soit a un point quelconque de U et soit D un disque ouvert de centre a entièrement contenu dans U; pour z 捻 D, désignons respectivement par A, M, P, Q les points d’affixes respectives:
Le théorème de MoreraLe théorème de Cauchy admet une réciproque, qui ne fait intervenir que des intégrales curvilignes le long de contours fermés très simples: le théorème de Morera affirme qu’une fonction f continue dans un ouvert U est analytique dans U si et seulement si son intégrale curviligne le long de tout rectangle, de côtés parallèles aux axes Ox et Oy , assez petit pour être entièrement contenu dans U est nulle. La condition nécessaire résulte du théorème de Cauchy; indiquons le principe de la démonstration de la réciproque. Soit a un point quelconque de U et soit D un disque ouvert de centre a entièrement contenu dans U; pour z 捻 D, désignons respectivement par A, M, P, Q les points d’affixes respectives: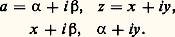 D’après l’hypothèse, les intégrales curvilignes de f le long des deux chemins APM et AQM sont égales; soit F(z ) cette valeur commune. On vérifie facilement que F admet dans D des dérivées partielles qui sont:
D’après l’hypothèse, les intégrales curvilignes de f le long des deux chemins APM et AQM sont égales; soit F(z ) cette valeur commune. On vérifie facilement que F admet dans D des dérivées partielles qui sont: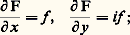 d’après les conditions de Cauchy-Riemann (6) ou (7), la fonction F est donc analytique, de dérivée au sens complexe f . Ainsi la fonction f , qui est, au voisinage de chaque point, la dérivée d’une fonction analytique, est analytique dans U.Le théorème de Morera peut servir à éliminer des «fausses» singularités. Par exemple, désignons par P+ et par P- les demi-plans ouverts Imz 礪 0 et Imz 麗 0; si f est une fonction continue dans un ouvert U qui est analytique dans chacun des ouverts U 惡 P+ et U 惡 P-, alors f est en fait analytique dans U tout entier. Il suffit de montrer que l’intégrale de f le long de tout rectangle de côtés parallèles aux axes est nulle et le seul cas où une démonstration est nécessaire est celui où ce rectangle ABCD coupe l’axe réel, c’est-à-dire rencontre à la fois P+ et P-; bornons-nous à de rapides indications géométriques. Introduisons, comme l’indique la figure 4, les segments opposés PQ et RS, parallèles et à une distance 﨎 de l’axe réel. Puisque f est analytique dans P+ et dans P-, les intégrales curvilignes de f le long des lignes brisées QABP et SCDR sont respectivement égales aux intégrales curvilignes de f le long des segments PQ et RS. La continuité de f entraîne alors que, lorsque 﨎 tend vers 0, les intégrales de f le long de PS et de RQ tendent vers 0, tandis que les intégrales le long des segments PQ et RS tendent vers des valeurs opposées (fig. 4). À la limite, on obtient bien que l’intégrale de f le long du rectangle ABCD est nulle.Le résultat qui précède permet d’établir le principe de symétrie de Schwarz, utilisé pour prolonger des fonctions analytiques (cf. FONCTIONS ANALYTIQUES – Fonctions elliptiques et modulaire). Soit U un ouvert connexe symétrique par rapport à une droite L; désignons par V l’intersection de U avec un des demi-plans fermés déterminés par L et par U1 l’intersection de U avec le demi-plan ouvert correspondant. Alors, toute fonction f continue dans V, analytique dans U1 et telle que f (U 惡 L) 說 L , où L est une droite, se prolonge (de manière unique car U est connexe) en une fonction analytique dans U tout entier (en faisant correspondre à des valeurs de z symétriques par rapport à L des valeurs de f (z ) symétriques par rapport à L ). En effet, par des transformations affines portant sur z et sur f (z ), on peut toujours se ramener au cas où L et L sont l’axe réel, U symétrique par rapport à l’axe réel, U1 = U 惡 P+ et f (z ) réel pour z 捻 U 惡 R. Il suffit alors de remarquer que la fonction g définie dans U tout entier par:
d’après les conditions de Cauchy-Riemann (6) ou (7), la fonction F est donc analytique, de dérivée au sens complexe f . Ainsi la fonction f , qui est, au voisinage de chaque point, la dérivée d’une fonction analytique, est analytique dans U.Le théorème de Morera peut servir à éliminer des «fausses» singularités. Par exemple, désignons par P+ et par P- les demi-plans ouverts Imz 礪 0 et Imz 麗 0; si f est une fonction continue dans un ouvert U qui est analytique dans chacun des ouverts U 惡 P+ et U 惡 P-, alors f est en fait analytique dans U tout entier. Il suffit de montrer que l’intégrale de f le long de tout rectangle de côtés parallèles aux axes est nulle et le seul cas où une démonstration est nécessaire est celui où ce rectangle ABCD coupe l’axe réel, c’est-à-dire rencontre à la fois P+ et P-; bornons-nous à de rapides indications géométriques. Introduisons, comme l’indique la figure 4, les segments opposés PQ et RS, parallèles et à une distance 﨎 de l’axe réel. Puisque f est analytique dans P+ et dans P-, les intégrales curvilignes de f le long des lignes brisées QABP et SCDR sont respectivement égales aux intégrales curvilignes de f le long des segments PQ et RS. La continuité de f entraîne alors que, lorsque 﨎 tend vers 0, les intégrales de f le long de PS et de RQ tendent vers 0, tandis que les intégrales le long des segments PQ et RS tendent vers des valeurs opposées (fig. 4). À la limite, on obtient bien que l’intégrale de f le long du rectangle ABCD est nulle.Le résultat qui précède permet d’établir le principe de symétrie de Schwarz, utilisé pour prolonger des fonctions analytiques (cf. FONCTIONS ANALYTIQUES – Fonctions elliptiques et modulaire). Soit U un ouvert connexe symétrique par rapport à une droite L; désignons par V l’intersection de U avec un des demi-plans fermés déterminés par L et par U1 l’intersection de U avec le demi-plan ouvert correspondant. Alors, toute fonction f continue dans V, analytique dans U1 et telle que f (U 惡 L) 說 L , où L est une droite, se prolonge (de manière unique car U est connexe) en une fonction analytique dans U tout entier (en faisant correspondre à des valeurs de z symétriques par rapport à L des valeurs de f (z ) symétriques par rapport à L ). En effet, par des transformations affines portant sur z et sur f (z ), on peut toujours se ramener au cas où L et L sont l’axe réel, U symétrique par rapport à l’axe réel, U1 = U 惡 P+ et f (z ) réel pour z 捻 U 惡 R. Il suffit alors de remarquer que la fonction g définie dans U tout entier par: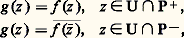 est continue dans U et analytique dans chacun des ouverts U 惡 P+ et U 惡 P-; remarquons que g prend des valeurs symétriques par rapport à l’axe réel en des points symétriques par rapport à l’axe réel.5. La formule intégrale de CauchyCette formule donne les valeurs d’une fonction analytique, sous forme d’une intégrale curviligne; en particulier, elle traduit le fait que les valeurs d’une fonction analytique à l’«intérieur» d’une courbe sont déterminées par les valeurs prises sur la courbe. Nous aurons tout d’abord besoin de préciser une notion de caractère géométrique, le «nombre de fois» où une courbe fermée «tourne» autour d’un point.L’indiceSoit 塚: I = [a , b ]C un lacet et soit 行 le complémentaire de la trajectoire 塚(I) de 塚. Pour tout z 捻 行, on appelle indice du point z par rapport au lacet 塚 le nombre:
est continue dans U et analytique dans chacun des ouverts U 惡 P+ et U 惡 P-; remarquons que g prend des valeurs symétriques par rapport à l’axe réel en des points symétriques par rapport à l’axe réel.5. La formule intégrale de CauchyCette formule donne les valeurs d’une fonction analytique, sous forme d’une intégrale curviligne; en particulier, elle traduit le fait que les valeurs d’une fonction analytique à l’«intérieur» d’une courbe sont déterminées par les valeurs prises sur la courbe. Nous aurons tout d’abord besoin de préciser une notion de caractère géométrique, le «nombre de fois» où une courbe fermée «tourne» autour d’un point.L’indiceSoit 塚: I = [a , b ]C un lacet et soit 行 le complémentaire de la trajectoire 塚(I) de 塚. Pour tout z 捻 行, on appelle indice du point z par rapport au lacet 塚 le nombre:
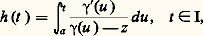 de telle sorte que j (z ; 塚) = h (b )/2 i 神, par définition de l’intégrale curviligne le long de 塚. Puisque e w = 1 si et seulement si w /2 i 神 est un entier (cf. EXPONENTIELLE ET LOGARITHME, chap. 4), il suffit d’établir que e -h(b) = 1.Posons:
de telle sorte que j (z ; 塚) = h (b )/2 i 神, par définition de l’intégrale curviligne le long de 塚. Puisque e w = 1 si et seulement si w /2 i 神 est un entier (cf. EXPONENTIELLE ET LOGARITHME, chap. 4), il suffit d’établir que e -h(b) = 1.Posons: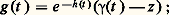 puisque:
puisque: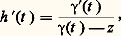 sauf en un nombre fini de points, on a:
sauf en un nombre fini de points, on a: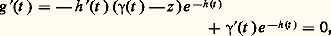 ce qui montre que la fonction continue g est constante, sur [a , b ]. En particulier, g (a ) = g (b ), d’où, puisque h (a ) = 0:
ce qui montre que la fonction continue g est constante, sur [a , b ]. En particulier, g (a ) = g (b ), d’où, puisque h (a ) = 0: La formule (23) montre facilement que, pour 塚 fixé, la fonction z 料 j (z ; 塚) est continue dans 行; puisqu’elle ne prend que des valeurs entières, elle est donc constante dans chaque composante connexe de 行. D’autre part, si 塚1 et 塚2 sont deux lacets homotopes dans le complémentaire de z , il résulte du théorème de Cauchy que j (z ; 塚1) = j (z ; 塚2), puisque 﨣 料 1/( 﨣 漣 z ) est analytique dans C 漣a; en particulier, si la trajectoire de 塚 est contenue dans un ouvert simplement connexe U, on a j (z ; 塚) = 0 pour tout z 殮 U. Il en résulte que j (z ; 塚) = 0 pour |z | assez grand et par suite dans toute la composante connexe non bornée de 行 = C 漣 塚(I). Si 塚: t 料 e int , n 捻 Z, est le cercle unité parcouru n fois, on a:
La formule (23) montre facilement que, pour 塚 fixé, la fonction z 料 j (z ; 塚) est continue dans 行; puisqu’elle ne prend que des valeurs entières, elle est donc constante dans chaque composante connexe de 行. D’autre part, si 塚1 et 塚2 sont deux lacets homotopes dans le complémentaire de z , il résulte du théorème de Cauchy que j (z ; 塚1) = j (z ; 塚2), puisque 﨣 料 1/( 﨣 漣 z ) est analytique dans C 漣a; en particulier, si la trajectoire de 塚 est contenue dans un ouvert simplement connexe U, on a j (z ; 塚) = 0 pour tout z 殮 U. Il en résulte que j (z ; 塚) = 0 pour |z | assez grand et par suite dans toute la composante connexe non bornée de 行 = C 漣 塚(I). Si 塚: t 料 e int , n 捻 Z, est le cercle unité parcouru n fois, on a: et par suite j (z ; 塚) = n pour |z | 麗 1, puisque le disque unité est connexe; puisque l’extérieur du disque unité est connexe, on a j (z ; 塚) = 0 pour |z | 礪 1. De manière générale, l’indice exprime le nombre algébrique de fois où le point 塚(t ) «tourne» autour de z lorsque t croît de a à b . Par exemple, sur la figure 5, on a j (u ; 塚) = 1, j (v; 塚) = 3, j (w ; 塚) = 2.La notion d’indice permet, en introduisant une nouvelle définition, de définir le cadre exact du théorème de Cauchy. Soit U un ouvert du plan; on dira que deux lacets 塚 et 塚 sont U-homologues si tout point du complémentaire de U a le même indice par rapport à ces deux lacets. Intuitivement, cela exprime que 塚 et 塚 «tournent» le même nombre de fois autour de tout point du complémentaire de U. On voit alors facilement que deux lacets homotopes dans U sont a fortiori U-homologues. Le théorème de Cauchy, sous sa forme la plus générale, que nous admettrons, affirme que, si 塚 et 塚 sont U-homologues, alors:
et par suite j (z ; 塚) = n pour |z | 麗 1, puisque le disque unité est connexe; puisque l’extérieur du disque unité est connexe, on a j (z ; 塚) = 0 pour |z | 礪 1. De manière générale, l’indice exprime le nombre algébrique de fois où le point 塚(t ) «tourne» autour de z lorsque t croît de a à b . Par exemple, sur la figure 5, on a j (u ; 塚) = 1, j (v; 塚) = 3, j (w ; 塚) = 2.La notion d’indice permet, en introduisant une nouvelle définition, de définir le cadre exact du théorème de Cauchy. Soit U un ouvert du plan; on dira que deux lacets 塚 et 塚 sont U-homologues si tout point du complémentaire de U a le même indice par rapport à ces deux lacets. Intuitivement, cela exprime que 塚 et 塚 «tournent» le même nombre de fois autour de tout point du complémentaire de U. On voit alors facilement que deux lacets homotopes dans U sont a fortiori U-homologues. Le théorème de Cauchy, sous sa forme la plus générale, que nous admettrons, affirme que, si 塚 et 塚 sont U-homologues, alors: pour toute fonction f analytique dans U.Formule intégrale de CauchySoit 塚 un lacet dans un domaine simplement connexe U; la formule intégrale de Cauchy exprime que, pour toute fonction f analytique dans U, on a:
pour toute fonction f analytique dans U.Formule intégrale de CauchySoit 塚 un lacet dans un domaine simplement connexe U; la formule intégrale de Cauchy exprime que, pour toute fonction f analytique dans U, on a: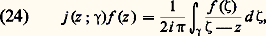 pour tout point z de U n’appartenant pas à la trajectoire de 塚.En effet, on voit facilement sur le développement en série entière de f au voisinage de z que la fonction g définie par:
pour tout point z de U n’appartenant pas à la trajectoire de 塚.En effet, on voit facilement sur le développement en série entière de f au voisinage de z que la fonction g définie par: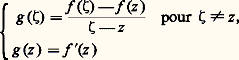 est analytique dans un voisinage de z , et, par suite, dans U tout entier. D’après le théorème de Cauchy (cf. chap. 4), l’intégrale curviligne de g le long de 塚 est donc nulle; soit, puisque z n’appartient pas à la trajectoire de 塚:
est analytique dans un voisinage de z , et, par suite, dans U tout entier. D’après le théorème de Cauchy (cf. chap. 4), l’intégrale curviligne de g le long de 塚 est donc nulle; soit, puisque z n’appartient pas à la trajectoire de 塚: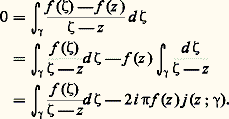 La formule de Cauchy est particulièrement intéressante lorsque 塚 est un cercle parcouru dans le sens direct ou rétrograde, car alors j (z ; 塚) = + 1 ou 漣 1 pour tout point z intérieur à ce cercle.La formule (24) exprime les valeurs d’une fonction analytique en fonction de sa restriction à la trajectoire d’un lacet 塚, qui est une fonction continue sur cette trajectoire. Réciproquement, on peut définir ainsi des fonctions analytiques. Plus précisément, soit 塚: IC un chemin (on ne suppose pas qu’il est fermé) et soit f une fonction continue sur la trajectoire 塚(I); alors la fonction:
La formule de Cauchy est particulièrement intéressante lorsque 塚 est un cercle parcouru dans le sens direct ou rétrograde, car alors j (z ; 塚) = + 1 ou 漣 1 pour tout point z intérieur à ce cercle.La formule (24) exprime les valeurs d’une fonction analytique en fonction de sa restriction à la trajectoire d’un lacet 塚, qui est une fonction continue sur cette trajectoire. Réciproquement, on peut définir ainsi des fonctions analytiques. Plus précisément, soit 塚: IC un chemin (on ne suppose pas qu’il est fermé) et soit f une fonction continue sur la trajectoire 塚(I); alors la fonction: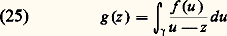 est analytique dans l’ouvert complémentaire de 塚(I). La démonstration consiste à établir, par des majorations au voisinage de chaque point, que l’on peut dériver (au sens complexe) sous le signe d’intégration, ce qui entraîne l’analyticité; ainsi, la dérivée n -ième au sens complexe est donnée par:
est analytique dans l’ouvert complémentaire de 塚(I). La démonstration consiste à établir, par des majorations au voisinage de chaque point, que l’on peut dériver (au sens complexe) sous le signe d’intégration, ce qui entraîne l’analyticité; ainsi, la dérivée n -ième au sens complexe est donnée par: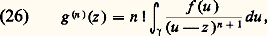 obtenu en dérivant n fois par rapport à z . En particulier, si f est analytique dans un ouvert simplement connexe U, on a, en combinant les deux résultats précédents:
obtenu en dérivant n fois par rapport à z . En particulier, si f est analytique dans un ouvert simplement connexe U, on a, en combinant les deux résultats précédents: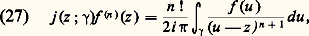 pour tout lacet 塚 de U et tout z 捻 U n’appartenant pas à la trajectoire de 塚.Suites convergentes de fonctions analytiquesDans le domaine réel, une limite uniforme de fonctions dérivables n’est pas nécessairement dérivable; en fait, le théorème de Weierstrass affirme même que toute fonction continue sur un intervalle borné [a , b ] est limite uniforme de polynômes (cf. représentation approximation des FONCTIONS). Mais, dans le cas complexe, la situation est tout à fait différente, et la formule intégrale de Cauchy permet d’obtenir des conditions très fortes de régularité par passage à la limite.La notion de convergence appropriée ici est la «convergence uniforme sur tout compact». Soit f 1, f 2, ..., f n , ... une suite de fonctions analytiques dans un ouvert U du plan complexe; on dit que la suite (f n ) converge uniformément sur tout compact vers une fonction f si tout point a 捻 U est centre d’un disque fermé inclus dans U sur lequel la suite (f n ) converge uniformément vers f , c’est-à-dire:
pour tout lacet 塚 de U et tout z 捻 U n’appartenant pas à la trajectoire de 塚.Suites convergentes de fonctions analytiquesDans le domaine réel, une limite uniforme de fonctions dérivables n’est pas nécessairement dérivable; en fait, le théorème de Weierstrass affirme même que toute fonction continue sur un intervalle borné [a , b ] est limite uniforme de polynômes (cf. représentation approximation des FONCTIONS). Mais, dans le cas complexe, la situation est tout à fait différente, et la formule intégrale de Cauchy permet d’obtenir des conditions très fortes de régularité par passage à la limite.La notion de convergence appropriée ici est la «convergence uniforme sur tout compact». Soit f 1, f 2, ..., f n , ... une suite de fonctions analytiques dans un ouvert U du plan complexe; on dit que la suite (f n ) converge uniformément sur tout compact vers une fonction f si tout point a 捻 U est centre d’un disque fermé inclus dans U sur lequel la suite (f n ) converge uniformément vers f , c’est-à-dire: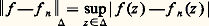 tend vers zéro pour n tendant vers l’infini. On peut alors affirmer (théorème dû à Karl Weierstrass) que la fonction limite f est analytique dans U; de plus, la suite (f n ) des dérivées converge uniformément sur tout compact vers la dérivée f de f . Soit en effet D 漣(a , r ) un disque fermé de centre a sur lequel la convergence est uniforme, et soit 塚 le cercle frontière |z 漣 a | = r parcouru une fois dans le sens direct. D’après la formule de Cauchy, on a:
tend vers zéro pour n tendant vers l’infini. On peut alors affirmer (théorème dû à Karl Weierstrass) que la fonction limite f est analytique dans U; de plus, la suite (f n ) des dérivées converge uniformément sur tout compact vers la dérivée f de f . Soit en effet D 漣(a , r ) un disque fermé de centre a sur lequel la convergence est uniforme, et soit 塚 le cercle frontière |z 漣 a | = r parcouru une fois dans le sens direct. D’après la formule de Cauchy, on a: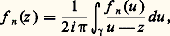 pour |z 漣 a | 麗 r . Puisque les fonctions (f n ) convergent uniformément vers f sur le cercle |z 漣 a | = r , un passage à la limite dans l’intégrale montre que:
pour |z 漣 a | 麗 r . Puisque les fonctions (f n ) convergent uniformément vers f sur le cercle |z 漣 a | = r , un passage à la limite dans l’intégrale montre que:
 une majoration facile de 1/(u 漣 z )2 montre alors que f n converge uniformément dans tout disque |z 漣 a | 諒 r , r 麗 r , vers:
une majoration facile de 1/(u 漣 z )2 montre alors que f n converge uniformément dans tout disque |z 漣 a | 諒 r , r 麗 r , vers: Les résultats précédents permettent de définir des fonctions analytiques à partir de séries ou de produits infinis de fonctions analytiques ou encore d’étendre (25) à des «chemins sans fin» (cf. fonction GAMMA).6. Points singuliers isolés et résidusOn se propose ici, dans une première approche vers les points singuliers, d’étudier le comportement d’une fonction analytique dans un disque pointé 0 麗 |z 漣 a | 麗 r , c’est-à-dire dans un disque ouvert privé de son centre; si f ne se prolonge pas en une fonction analytique dans le disque entier, on dira que a est un point singulier (isolé) pour f .La série de LaurentUn disque pointé 0 麗|z 漣 a | 麗r est un cas particulier d’une couronne ouverte r 1 麗|z 漣 a | 麗r 2; on va obtenir pour une fonction analytique dans une telle couronne S un développement en série généralisant le développement en série entière de centre a , valable seulement pour les fonctions analytiques dans tout un disque de centre a .Il nous faut d’abord étendre la formule de Cauchy qui n’est pas applicable directement, puisque S n’est pas simplement connexe. Soit r et r tels que r 1 麗 r 麗 r 麗 r 2 et soit 塚 et 塚 les cercles de centre a et de rayons r et r parcourus une fois dans le sens direct (fig. 6). On voit comme ci-dessus que, pour r 麗 |z 漣 a | 麗 r , la fonction g définie par:
Les résultats précédents permettent de définir des fonctions analytiques à partir de séries ou de produits infinis de fonctions analytiques ou encore d’étendre (25) à des «chemins sans fin» (cf. fonction GAMMA).6. Points singuliers isolés et résidusOn se propose ici, dans une première approche vers les points singuliers, d’étudier le comportement d’une fonction analytique dans un disque pointé 0 麗 |z 漣 a | 麗 r , c’est-à-dire dans un disque ouvert privé de son centre; si f ne se prolonge pas en une fonction analytique dans le disque entier, on dira que a est un point singulier (isolé) pour f .La série de LaurentUn disque pointé 0 麗|z 漣 a | 麗r est un cas particulier d’une couronne ouverte r 1 麗|z 漣 a | 麗r 2; on va obtenir pour une fonction analytique dans une telle couronne S un développement en série généralisant le développement en série entière de centre a , valable seulement pour les fonctions analytiques dans tout un disque de centre a .Il nous faut d’abord étendre la formule de Cauchy qui n’est pas applicable directement, puisque S n’est pas simplement connexe. Soit r et r tels que r 1 麗 r 麗 r 麗 r 2 et soit 塚 et 塚 les cercles de centre a et de rayons r et r parcourus une fois dans le sens direct (fig. 6). On voit comme ci-dessus que, pour r 麗 |z 漣 a | 麗 r , la fonction g définie par: est analytique dans S. Puisque les lacets 塚 et 塚 sont manifestement homotopes dans S, le théorème de Cauchy (cf. chap. 4) affirme que les intégrales de g le long de 塚 et 塚 sont égales. On a donc:
est analytique dans S. Puisque les lacets 塚 et 塚 sont manifestement homotopes dans S, le théorème de Cauchy (cf. chap. 4) affirme que les intégrales de g le long de 塚 et 塚 sont égales. On a donc: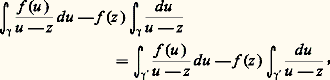
 qui généralise (24).Remarquons alors que (en supposant, dans le calcul qui suit, a = 0 pour simplifier, ce qui ne retire aucune généralité), d’après le choix de z , r 麗 |z | 麗 r , la série:
qui généralise (24).Remarquons alors que (en supposant, dans le calcul qui suit, a = 0 pour simplifier, ce qui ne retire aucune généralité), d’après le choix de z , r 麗 |z | 麗 r , la série: converge uniformément pour |u | = r , car alors |u /z | = |z |/r 麗 1; on peut donc intégrer terme à terme sur 塚 et on obtient:
converge uniformément pour |u | = r , car alors |u /z | = |z |/r 麗 1; on peut donc intégrer terme à terme sur 塚 et on obtient: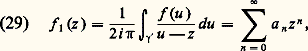 avec:
avec: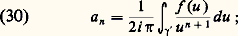 en fait, ces coefficients a n ne dépendent pas de r , car la fonction f (u )/u n+1 est analytique dans S et, par suite, d’après le théorème de Cauchy, on peut remplacer 塚 par n’importe quel cercle concentrique (contenu dans S) parcouru dans le sens direct, puisqu’il est homotope à 塚 . Ainsi la série entière définie dans (29) converge pour tout z de module 麗 r 2; donc elle a un rayon de convergence 閭 r 2 et, par suite, f 1 se prolonge en une fonction analytique pour |z | 麗 r 2 (que nous désignerons encore par f 1). Remarquons qu’on aurait pu obtenir le résultat qui précède sans développer 1/(u 漣 z ) en série: d’après (25), la fonction f 1 définie par l’intégrale (29) est analytique pour |z | 麗 r ; d’après le théorème 4 du chapitre 2 elle est donc développable en série entière et les intégrales (10) ne sont autres que des intégrales curvilignes du type (30) que l’on a explicitées en revenant à la définition. De même, la série:
en fait, ces coefficients a n ne dépendent pas de r , car la fonction f (u )/u n+1 est analytique dans S et, par suite, d’après le théorème de Cauchy, on peut remplacer 塚 par n’importe quel cercle concentrique (contenu dans S) parcouru dans le sens direct, puisqu’il est homotope à 塚 . Ainsi la série entière définie dans (29) converge pour tout z de module 麗 r 2; donc elle a un rayon de convergence 閭 r 2 et, par suite, f 1 se prolonge en une fonction analytique pour |z | 麗 r 2 (que nous désignerons encore par f 1). Remarquons qu’on aurait pu obtenir le résultat qui précède sans développer 1/(u 漣 z ) en série: d’après (25), la fonction f 1 définie par l’intégrale (29) est analytique pour |z | 麗 r ; d’après le théorème 4 du chapitre 2 elle est donc développable en série entière et les intégrales (10) ne sont autres que des intégrales curvilignes du type (30) que l’on a explicitées en revenant à la définition. De même, la série: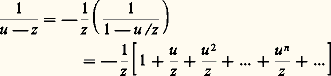
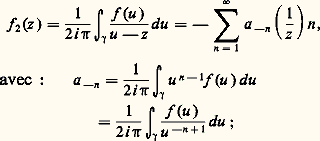 par le même raisonnement que ci-dessus, on voit alors que ces coefficients ne dépendent pas de r pour r 1 麗 r 麗 r 2 et que la série de terme général a -n z -n est convergente pour |z | 礪 r 1. Sa somme, que nous désignerons encore par f 2, est donc une fonction analytique pour |z | 礪 r 1.Revenant au cas d’un point a 捻 C, énonçons les résultats précédents. Soit S une couronne r 1 麗 |z 漣 a | 麗 r 2; toute fonction f analytique dans S peut s’écrire:
par le même raisonnement que ci-dessus, on voit alors que ces coefficients ne dépendent pas de r pour r 1 麗 r 麗 r 2 et que la série de terme général a -n z -n est convergente pour |z | 礪 r 1. Sa somme, que nous désignerons encore par f 2, est donc une fonction analytique pour |z | 礪 r 1.Revenant au cas d’un point a 捻 C, énonçons les résultats précédents. Soit S une couronne r 1 麗 |z 漣 a | 麗 r 2; toute fonction f analytique dans S peut s’écrire: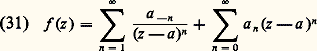 où la première série converge pour |z 漣 a | 礪 r 1 et la seconde pour |z 漣 a | 麗 r 2; leurs sommes sont donc des fonctions analytiques pour |z 漣 a | 礪 r 1 et |z 漣 a | 麗 r 2 respectivement. Pour tout n entier relatif, les coefficients a n sont donnés par:
où la première série converge pour |z 漣 a | 礪 r 1 et la seconde pour |z 漣 a | 麗 r 2; leurs sommes sont donc des fonctions analytiques pour |z 漣 a | 礪 r 1 et |z 漣 a | 麗 r 2 respectivement. Pour tout n entier relatif, les coefficients a n sont donnés par: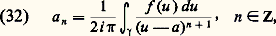 où 塚 est un cercle quelconque de centre a et de rayon r , r 1 麗 r 麗 r 2, parcouru une fois dans le sens direct.Points singuliersSoit f une fonction analytique dans un disque pointé 0 麗 |z 漣 a | 麗 r . Un tel disque pointé étant un cas particulier de couronne, f admet un développement du type (31). Remarquons qu’ici la série entière:
où 塚 est un cercle quelconque de centre a et de rayon r , r 1 麗 r 麗 r 2, parcouru une fois dans le sens direct.Points singuliersSoit f une fonction analytique dans un disque pointé 0 麗 |z 漣 a | 麗 r . Un tel disque pointé étant un cas particulier de couronne, f admet un développement du type (31). Remarquons qu’ici la série entière: converge pour tout 﨣 捻 C; u est donc une fonction analytique dans tout le plan telle que u (0) = 0. On dit que:
converge pour tout 﨣 捻 C; u est donc une fonction analytique dans tout le plan telle que u (0) = 0. On dit que: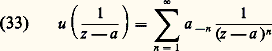 est la partie singulière de la fonction f au point a . D’après (31), la fonction f est donc somme de sa partie singulière et d’une fonction analytique dans tout le disque |z 漣 a | 麗 r .Si u = 0, la formule (31) montre que f est somme d’une série entière pour |z 漣 a | 麗 r et, par suite, se prolonge par continuité en une fonction analytique dans tout ce disque: a n’est pas un «vrai» point singulier; on dit que c’est un point régulier . Pour u 0, on dit que a est un point singulier isolé .Si u est un polynôme de degré m 閭 1, on dit que a est un pôle d’ordre m . Remarquons qu’alors la fonction (z 漣 a )m f (z ) se prolonge en une fonction h analytique dans le disque |z 漣 a | 麗 r et que:
est la partie singulière de la fonction f au point a . D’après (31), la fonction f est donc somme de sa partie singulière et d’une fonction analytique dans tout le disque |z 漣 a | 麗 r .Si u = 0, la formule (31) montre que f est somme d’une série entière pour |z 漣 a | 麗 r et, par suite, se prolonge par continuité en une fonction analytique dans tout ce disque: a n’est pas un «vrai» point singulier; on dit que c’est un point régulier . Pour u 0, on dit que a est un point singulier isolé .Si u est un polynôme de degré m 閭 1, on dit que a est un pôle d’ordre m . Remarquons qu’alors la fonction (z 漣 a )m f (z ) se prolonge en une fonction h analytique dans le disque |z 漣 a | 麗 r et que: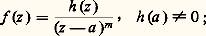 cela entraîne que |f (z )|秊 pour za . Plus généralement, si f et g sont analytiques dans un voisinage de a avec f (a ) 0 et a zéro d’ordre m de g (cf. chap. 1), alors f /g a un pôle d’ordre m en a , car on peut écrire g (z ) = (z 漣 a )m h (z ), avec h (z ) 0, d’où f /h est analytique, dans un disque de centre a . Ce qui précède conduit à la notion de fonction méromorphe: Soit U un ouvert du plan et P un sous-ensemble fermé de U dont tous les points sont isolés; on dit qu’une fonction analytique dans U 漣 P est méromorphe dans U si les points de P sont des points réguliers ou des pôles (on peut d’ailleurs se ramener à ce seul cas en prolongeant F par continuité aux points réguliers; P est alors l’ensemble des pôles de la fonction méromorphe). Remarquons que cela revient à dire que tout point de U est centre d’un disque pointé inclus dans U dans lequel f est quotient de deux fonctions analytiques dans le disque tout entier.Examinons enfin le cas où il existe une infinité d’entiers positifs n tels que a -n 0; on dit alors que a est un point singulier essentiel . Par exemple, la fonction:
cela entraîne que |f (z )|秊 pour za . Plus généralement, si f et g sont analytiques dans un voisinage de a avec f (a ) 0 et a zéro d’ordre m de g (cf. chap. 1), alors f /g a un pôle d’ordre m en a , car on peut écrire g (z ) = (z 漣 a )m h (z ), avec h (z ) 0, d’où f /h est analytique, dans un disque de centre a . Ce qui précède conduit à la notion de fonction méromorphe: Soit U un ouvert du plan et P un sous-ensemble fermé de U dont tous les points sont isolés; on dit qu’une fonction analytique dans U 漣 P est méromorphe dans U si les points de P sont des points réguliers ou des pôles (on peut d’ailleurs se ramener à ce seul cas en prolongeant F par continuité aux points réguliers; P est alors l’ensemble des pôles de la fonction méromorphe). Remarquons que cela revient à dire que tout point de U est centre d’un disque pointé inclus dans U dans lequel f est quotient de deux fonctions analytiques dans le disque tout entier.Examinons enfin le cas où il existe une infinité d’entiers positifs n tels que a -n 0; on dit alors que a est un point singulier essentiel . Par exemple, la fonction: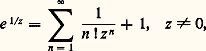 admet 0 pour point singulier essentiel. Un théorème dû à Émile Picard, précisant un théorème plus élémentaire de Weierstrass, décrit le comportement d’une fonction analytique autour d’un point singulier essentiel: Si a est un point singulier essentiel pour une fonction f , alors, dans tout disque pointé de centre a , la fonction f prend toutes les valeurs complexes, sauf au plus une; par exemple, la fonction e 1/z prend toutes les valeurs sauf 0 dans tout disque pointé de centre O.Le théorème des résidusSoit U un ouvert et a 1, a 2, ..., a n des points distincts de U. Si f est une fonction analytique dans U = U 漣a 1, a 2, ..., a n, désignons par v 1, v 2, ..., v n les parties singulières de f en a 1, a 2, ..., a n respectivement; ainsi, la fonction v k est analytique dans le plan complexe privé du point a k . La fonction:
admet 0 pour point singulier essentiel. Un théorème dû à Émile Picard, précisant un théorème plus élémentaire de Weierstrass, décrit le comportement d’une fonction analytique autour d’un point singulier essentiel: Si a est un point singulier essentiel pour une fonction f , alors, dans tout disque pointé de centre a , la fonction f prend toutes les valeurs complexes, sauf au plus une; par exemple, la fonction e 1/z prend toutes les valeurs sauf 0 dans tout disque pointé de centre O.Le théorème des résidusSoit U un ouvert et a 1, a 2, ..., a n des points distincts de U. Si f est une fonction analytique dans U = U 漣a 1, a 2, ..., a n, désignons par v 1, v 2, ..., v n les parties singulières de f en a 1, a 2, ..., a n respectivement; ainsi, la fonction v k est analytique dans le plan complexe privé du point a k . La fonction: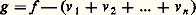 est alors analytique dans U et sa partie singulière en chacun des points a k est nulle; elle se prolonge donc en une fonction, que nous désignerons encore par g , analytique dans U tout entier. Si U est simplement connexe, le théorème de Cauchy affirme que l’intégrale de g le long de tout lacet 塚 est nulle, soit, si aucun des a k n’appartient à la trajectoire de 塚:
est alors analytique dans U et sa partie singulière en chacun des points a k est nulle; elle se prolonge donc en une fonction, que nous désignerons encore par g , analytique dans U tout entier. Si U est simplement connexe, le théorème de Cauchy affirme que l’intégrale de g le long de tout lacet 塚 est nulle, soit, si aucun des a k n’appartient à la trajectoire de 塚: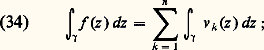 ainsi, pour calculer l’intégrale de f , il suffit de calculer les intégrales des v k . Effectuons ce calcul. Soit donc:
ainsi, pour calculer l’intégrale de f , il suffit de calculer les intégrales des v k . Effectuons ce calcul. Soit donc: une fonction analytique dans tout le plan et 塚: IC un lacet dont la trajectoire 塚 (I) ne contient pas un point a ; la série:
une fonction analytique dans tout le plan et 塚: IC un lacet dont la trajectoire 塚 (I) ne contient pas un point a ; la série: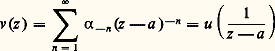 converge uniformément pour z = 塚(t ), t 捻 I, et, par suite, on peut intégrer terme à terme cette série sur le lacet 塚. Or, pour n 閭 2, la fonction (z 漣 a )-n admet une primitive (1 漣 n )(z 漣 a )1-n dans C 漣a et, par suite, son intégrale le long de 塚 est nulle; il reste seulement le terme en 1/(z 漣 a ), qui introduit l’indice du point a par rapport au lacet 塚:
converge uniformément pour z = 塚(t ), t 捻 I, et, par suite, on peut intégrer terme à terme cette série sur le lacet 塚. Or, pour n 閭 2, la fonction (z 漣 a )-n admet une primitive (1 漣 n )(z 漣 a )1-n dans C 漣a et, par suite, son intégrale le long de 塚 est nulle; il reste seulement le terme en 1/(z 漣 a ), qui introduit l’indice du point a par rapport au lacet 塚: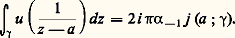 On voit donc l’importance du coefficient de 1/(z 漣 a ) dans la partie singulière au point a ; on l’appelle le résidu de f au point a , et on le note Res (a ; f ). Ce qui précède permet d’énoncer le théorème des résidus sous sa forme générale: Soit U un ouvert simplement connexe et a 1, ..., a n des points distincts de U; pour toute fonction f analytique dans:
On voit donc l’importance du coefficient de 1/(z 漣 a ) dans la partie singulière au point a ; on l’appelle le résidu de f au point a , et on le note Res (a ; f ). Ce qui précède permet d’énoncer le théorème des résidus sous sa forme générale: Soit U un ouvert simplement connexe et a 1, ..., a n des points distincts de U; pour toute fonction f analytique dans: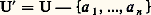 et tout lacet 塚 de U , on a la formule des résidus :
et tout lacet 塚 de U , on a la formule des résidus :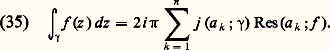 Cette formule est encore valable lorsque f est une fonction méromorphe dans l’ouvert simplement connexe U; soit P l’ensemble des pôles de f . Comme P n’a que des points isolés dans U, pour tout lacet 塚 de U 漣 P, l’ensemble des a 捻 P tels que j (a ; 塚) 0 est fini. Dans ces conditions, on a:
Cette formule est encore valable lorsque f est une fonction méromorphe dans l’ouvert simplement connexe U; soit P l’ensemble des pôles de f . Comme P n’a que des points isolés dans U, pour tout lacet 塚 de U 漣 P, l’ensemble des a 捻 P tels que j (a ; 塚) 0 est fini. Dans ces conditions, on a: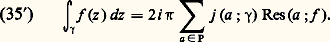 Un exemple de calculLa formule des résidus permet le calcul explicite de nombreuses intégrales. Donnons un exemple en calculant la transformée de Fourier de la fraction rationnelle R(x ) = 1/(x 2 + a 2), où a est un nombre complexe de partie réelle 礪 0. Il s’agit donc de calculer l’intégrale:
Un exemple de calculLa formule des résidus permet le calcul explicite de nombreuses intégrales. Donnons un exemple en calculant la transformée de Fourier de la fraction rationnelle R(x ) = 1/(x 2 + a 2), où a est un nombre complexe de partie réelle 礪 0. Il s’agit donc de calculer l’intégrale: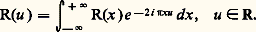 Considérons la fonction:
Considérons la fonction: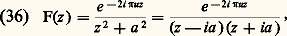 qui est méromorphe dans tout le plan et admet ia et 漣 ia comme pôles d’ordre 1. Calculons les résidus en ces points.De manière générale, si F(z ) = P(z )/Q(z ), où P et Q sont analytiques dans un disque de centre b , P(b ) 0 et b racine simple de Q, on a vu que:
qui est méromorphe dans tout le plan et admet ia et 漣 ia comme pôles d’ordre 1. Calculons les résidus en ces points.De manière générale, si F(z ) = P(z )/Q(z ), où P et Q sont analytiques dans un disque de centre b , P(b ) 0 et b racine simple de Q, on a vu que: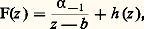
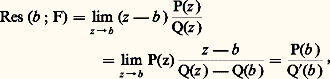 puisque Q(b ) = 0. Dans notre cas, on a donc, F étant la fonction (36):
puisque Q(b ) = 0. Dans notre cas, on a donc, F étant la fonction (36):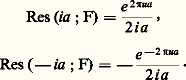 Dans le calcul qui suit, on est alors amené à distinguer deux cas, suivant que u 閭 0 ou u 諒 0. Pour u 閭 0, appliquons la formule des résidus à l’intégrale de F le long du lacet constitué par le segment [ 漣 R, R] de l’axe réel et par le demi-cercle 臨R de centre O et de rayon R, R 礪 |a |, du demi-plan inférieur (fig. 7). L’indice de ia est égal à 0 et l’indice de 漣 ia est égal à 漣 1. On a donc:
Dans le calcul qui suit, on est alors amené à distinguer deux cas, suivant que u 閭 0 ou u 諒 0. Pour u 閭 0, appliquons la formule des résidus à l’intégrale de F le long du lacet constitué par le segment [ 漣 R, R] de l’axe réel et par le demi-cercle 臨R de centre O et de rayon R, R 礪 |a |, du demi-plan inférieur (fig. 7). L’indice de ia est égal à 0 et l’indice de 漣 ia est égal à 漣 1. On a donc: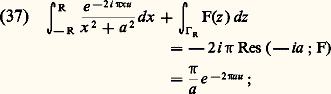 or, sur 臨R, on a:
or, sur 臨R, on a: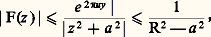 car |e x+iy | = e x et y 諒 0; la majoration (19) montre alors que l’intégrale de F le long de 臨R tend vers 0 quand R tend vers l’infini, puisque:
car |e x+iy | = e x et y 諒 0; la majoration (19) montre alors que l’intégrale de F le long de 臨R tend vers 0 quand R tend vers l’infini, puisque: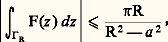 d’où, par passage à la limite dans (37):
d’où, par passage à la limite dans (37): Pour u 諒 0, on intègre sur le lacet constitué par le segment [ 漣 R, R] et le demi-cercle 臨 R orienté comme l’indique la figure 7. L’indice de ia est cette fois égal à + 1, tandis que l’indice de 漣 ia est nul. On voit, comme ci-dessus, que l’intégrale curviligne de F le long de 臨 R tend vers 0 pour R tendant vers l’infini et on obtient:
Pour u 諒 0, on intègre sur le lacet constitué par le segment [ 漣 R, R] et le demi-cercle 臨 R orienté comme l’indique la figure 7. L’indice de ia est cette fois égal à + 1, tandis que l’indice de 漣 ia est nul. On voit, comme ci-dessus, que l’intégrale curviligne de F le long de 臨 R tend vers 0 pour R tendant vers l’infini et on obtient: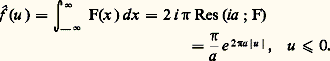 En résumé, on a donc:
En résumé, on a donc: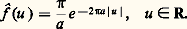 Compteur logarithmiqueSoit f une fonction méromorphe non nulle dans un ouvert simplement connexe U, soit N l’ensemble de ses zéros et P l’ensemble de ses pôles. Alors f /f est une fonction méromorphe dans U et ses pôles, qui sont tous simples, sont les éléments de N 聆 P.En outre, si a 捻 N, on a:
Compteur logarithmiqueSoit f une fonction méromorphe non nulle dans un ouvert simplement connexe U, soit N l’ensemble de ses zéros et P l’ensemble de ses pôles. Alors f /f est une fonction méromorphe dans U et ses pôles, qui sont tous simples, sont les éléments de N 聆 P.En outre, si a 捻 N, on a:
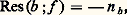 塚 de U 漣 (P 聆 N), on a:
塚 de U 漣 (P 聆 N), on a: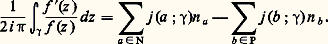 C’est pourquoi cette fonction s’apelle compteur logarithmique des zéros et des pôles de f .En particulier, si f est holomorphe dans U et si 塚 est le bord d’un disque contenu dans U 漣 N:
C’est pourquoi cette fonction s’apelle compteur logarithmique des zéros et des pôles de f .En particulier, si f est holomorphe dans U et si 塚 est le bord d’un disque contenu dans U 漣 N: où N size=1塚 est l’ensemble des zéros intérieurs au disque.Cette formule permet en particulier de déterminer le nombre de zéros d’un polynôme, comptés avec leur ordre de multiplicité, contenus dans un disque donné.Comme le compteur logarithmique dépend continûment des coefficients du polynôme, on en déduit que les racines d’un polynôme dépendent continûment des coefficients de ce polynôme (théorème de Weierstrass).De manière semblable, on peut utiliser le compteur logarithmique pour établir des propriétés du spectre d’un endomorphisme d’un espace vectoriel de dimension finie sur C (continuité des racines du polynôme caractéristique).7. Prolongement analytiqueOn se propose d’étudier ici la possibilité de prolonger une fonction f analytique dans un ouvert U à un ouvert plus grand. Pour tout point a 捻 U, la série de Taylor de f en a converge dans le plus grand disque ouvert D contenu dans U (cf. chap. 2); mais, comme on l’a déjà signalé ci-dessus, il se peut fort bien que le disque de convergence de cette série «déborde» de U. La somme de la série dans est alors une fonction analytique dans qui, d’après le principe du prolongement analytique (cf. chap. 1), coïncide avec f dans la composante connexe de U 惡 qui contient D. Cependant, si U 惡 n’est pas connexe, on ne peut pas affirmer en général que f se prolonge en une fonction analytique dans U 聆 . Prenons pour exemple, pour U, le plan complexe privé des nombres réels négatifs ou nul U = C 漣 R- et, pour f , la détermination principale du logarithme (cf. chap. 4). Pour z 0 = x 0 + iy 0, x 0 麗 0, y 0 礪 0, le disque de convergence de la série de Taylor de ln z en z 0 est le disque de centre z 0 qui passe par O, car la dérivée 1/z de ln z est analytique dans C = C 漣O (fig. 8). Ici 惡 U a deux composantes connexes et la somme de la série de Taylor en z 0 n’est pas égale à f (z ) pour z 捻 惡 U, Im z 麗 0, car Im (ln z ) = Arg z subit une discontinuité en «traversant» R- 惡 , ce qui exclut la possibilité de prolonger f à U 聆 . L’examen de ces phénomènes a priori surprenants conduit à des extensions de la notion de fonction analytique et aux surfaces de Riemann. Pour éviter des difficultés du type précédent, nous raisonnerons ici sur des disques, car l’intersection de deux disques est toujours connexe.Points singuliers et points réguliersSoit f une fonction analytique dans un disque ouvert D; on dira qu’un point frontière u est un point régulier pour f s’il existe un disque ouvert D1 de centre u et une fonction g analytique dans D1 qui coïncide avec f dans D 聆 D1. On peut alors prolonger f en une fonction analytique dans D 聆 D1, d’après le principe du prolongement analytique. Dans le cas contraire, on dit que u est un point singulier pour f . Il est clair que les points réguliers forment un ouvert de la frontière de D.Remarquons que le fait, pour u , d’être un point régulier ou singulier n’a rien à voir avec la nature de la convergence de la série de Taylor de f en u . Par exemple,
où N size=1塚 est l’ensemble des zéros intérieurs au disque.Cette formule permet en particulier de déterminer le nombre de zéros d’un polynôme, comptés avec leur ordre de multiplicité, contenus dans un disque donné.Comme le compteur logarithmique dépend continûment des coefficients du polynôme, on en déduit que les racines d’un polynôme dépendent continûment des coefficients de ce polynôme (théorème de Weierstrass).De manière semblable, on peut utiliser le compteur logarithmique pour établir des propriétés du spectre d’un endomorphisme d’un espace vectoriel de dimension finie sur C (continuité des racines du polynôme caractéristique).7. Prolongement analytiqueOn se propose d’étudier ici la possibilité de prolonger une fonction f analytique dans un ouvert U à un ouvert plus grand. Pour tout point a 捻 U, la série de Taylor de f en a converge dans le plus grand disque ouvert D contenu dans U (cf. chap. 2); mais, comme on l’a déjà signalé ci-dessus, il se peut fort bien que le disque de convergence de cette série «déborde» de U. La somme de la série dans est alors une fonction analytique dans qui, d’après le principe du prolongement analytique (cf. chap. 1), coïncide avec f dans la composante connexe de U 惡 qui contient D. Cependant, si U 惡 n’est pas connexe, on ne peut pas affirmer en général que f se prolonge en une fonction analytique dans U 聆 . Prenons pour exemple, pour U, le plan complexe privé des nombres réels négatifs ou nul U = C 漣 R- et, pour f , la détermination principale du logarithme (cf. chap. 4). Pour z 0 = x 0 + iy 0, x 0 麗 0, y 0 礪 0, le disque de convergence de la série de Taylor de ln z en z 0 est le disque de centre z 0 qui passe par O, car la dérivée 1/z de ln z est analytique dans C = C 漣O (fig. 8). Ici 惡 U a deux composantes connexes et la somme de la série de Taylor en z 0 n’est pas égale à f (z ) pour z 捻 惡 U, Im z 麗 0, car Im (ln z ) = Arg z subit une discontinuité en «traversant» R- 惡 , ce qui exclut la possibilité de prolonger f à U 聆 . L’examen de ces phénomènes a priori surprenants conduit à des extensions de la notion de fonction analytique et aux surfaces de Riemann. Pour éviter des difficultés du type précédent, nous raisonnerons ici sur des disques, car l’intersection de deux disques est toujours connexe.Points singuliers et points réguliersSoit f une fonction analytique dans un disque ouvert D; on dira qu’un point frontière u est un point régulier pour f s’il existe un disque ouvert D1 de centre u et une fonction g analytique dans D1 qui coïncide avec f dans D 聆 D1. On peut alors prolonger f en une fonction analytique dans D 聆 D1, d’après le principe du prolongement analytique. Dans le cas contraire, on dit que u est un point singulier pour f . Il est clair que les points réguliers forment un ouvert de la frontière de D.Remarquons que le fait, pour u , d’être un point régulier ou singulier n’a rien à voir avec la nature de la convergence de la série de Taylor de f en u . Par exemple,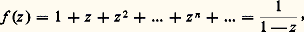 pour |z | 麗 1, est analytique dans D(0, 1), et tous les points du cercle |z | = 1, sauf le point z = 1, sont des points réguliers, bien que la série diverge en tout point de ce cercle. On peut montrer que, si D est le disque de convergence d’une série entière de somme f , il existe au moins un point singulier pour f , sur sa frontière, mais il se peut que tous les points frontières soient des points singuliers (séries «lacunaires»); on dit alors que D est le domaine naturel d’existence de la fonction, car, dans ce cas, on ne peut pas la prolonger en une fonction analytique dans un ouvert connexe plus grand.Éléments analytiquesPour étudier les problèmes posés par le prolongement analytique, nous introduirons une nouvelle notion due, sous cette forme, à Weierstrass.On appelle élément de fonction analytique , ou, en abrégé, élément analytique de centre a le couple (a , S) d’un nombre complexe a et d’une série entière S (de centre a ) de rayon de convergence strictement positif; par abus de langage, on désignera encore par S, dans ce qui suit, la somme de la série S dans son disque de convergence. Par exemple, toute fonction analytique dans un ouvert U définit un élément analytique de centre a en tout point a 捻 U.On dit que deux éléments analytiques (a , S) et (b , T) sont le prolongement analytique direct l’un de l’autre si leurs disques de convergence ont une intersection non vide et si S et T coïncident dans cette intersection. L’idée est de chercher à «prolonger» un élément analytique (a , S) en construisant des «chaînes»:
pour |z | 麗 1, est analytique dans D(0, 1), et tous les points du cercle |z | = 1, sauf le point z = 1, sont des points réguliers, bien que la série diverge en tout point de ce cercle. On peut montrer que, si D est le disque de convergence d’une série entière de somme f , il existe au moins un point singulier pour f , sur sa frontière, mais il se peut que tous les points frontières soient des points singuliers (séries «lacunaires»); on dit alors que D est le domaine naturel d’existence de la fonction, car, dans ce cas, on ne peut pas la prolonger en une fonction analytique dans un ouvert connexe plus grand.Éléments analytiquesPour étudier les problèmes posés par le prolongement analytique, nous introduirons une nouvelle notion due, sous cette forme, à Weierstrass.On appelle élément de fonction analytique , ou, en abrégé, élément analytique de centre a le couple (a , S) d’un nombre complexe a et d’une série entière S (de centre a ) de rayon de convergence strictement positif; par abus de langage, on désignera encore par S, dans ce qui suit, la somme de la série S dans son disque de convergence. Par exemple, toute fonction analytique dans un ouvert U définit un élément analytique de centre a en tout point a 捻 U.On dit que deux éléments analytiques (a , S) et (b , T) sont le prolongement analytique direct l’un de l’autre si leurs disques de convergence ont une intersection non vide et si S et T coïncident dans cette intersection. L’idée est de chercher à «prolonger» un élément analytique (a , S) en construisant des «chaînes»: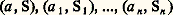 telles que deux éléments analytiques consécutifs quelconques soient prolongements directs l’un de l’autre.Prolongement le long d’un cheminSoit 塚: [0, 1]C un chemin; on dit qu’un élément analytique (b , S), de centre b = 塚(1), est le prolongement analytique le long de 塚 d’un élément (a , S) de centre a = 塚(0) s’il existe une chaîne (au sens précédent):
telles que deux éléments analytiques consécutifs quelconques soient prolongements directs l’un de l’autre.Prolongement le long d’un cheminSoit 塚: [0, 1]C un chemin; on dit qu’un élément analytique (b , S), de centre b = 塚(1), est le prolongement analytique le long de 塚 d’un élément (a , S) de centre a = 塚(0) s’il existe une chaîne (au sens précédent): d’éléments analytiques centrés sur 塚([0,1]) dont les disques de convergence recouvrent cette trajectoire.Si 塚 est un chemin d’origine a et (a , S) un élément analytique, il n’est pas toujours possible de prolonger cet élément analytique le long de 塚 (par exemple, si la trajectoire de 塚 contient un point singulier de S), mais on peut montrer que, si cela est possible, il y a unicité du prolongement. Par contre, ce prolongement ne dépend pas en général seulement de l’origine et de l’extrémité de 塚. Considérons, par exemple, l’élément analytique (1, S), où S est la série de Taylor au point 1 de la détermination principale du logarithme, S(1) = 0. Le prolongement analytique le long des deux demi-cercles |z | = 1, Im z 礪 0 et Im z 麗 0, respectivement de 1 vers 漣 1, donne (face=F0019 漣 1, T) et (face=F0019 漣 1, U) où T et U sont des déterminations du logarithme dans D(face=F0019 漣 1, 1) qui diffèrent de 2 i 神, car:
d’éléments analytiques centrés sur 塚([0,1]) dont les disques de convergence recouvrent cette trajectoire.Si 塚 est un chemin d’origine a et (a , S) un élément analytique, il n’est pas toujours possible de prolonger cet élément analytique le long de 塚 (par exemple, si la trajectoire de 塚 contient un point singulier de S), mais on peut montrer que, si cela est possible, il y a unicité du prolongement. Par contre, ce prolongement ne dépend pas en général seulement de l’origine et de l’extrémité de 塚. Considérons, par exemple, l’élément analytique (1, S), où S est la série de Taylor au point 1 de la détermination principale du logarithme, S(1) = 0. Le prolongement analytique le long des deux demi-cercles |z | = 1, Im z 礪 0 et Im z 麗 0, respectivement de 1 vers 漣 1, donne (face=F0019 漣 1, T) et (face=F0019 漣 1, U) où T et U sont des déterminations du logarithme dans D(face=F0019 漣 1, 1) qui diffèrent de 2 i 神, car: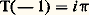 et:
et: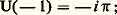 si on considère aussi, à partir de ce même élément (1, S), les prolongements analytiques le long de tous les chemins d’origine 1 et d’extrémité 漣 1 qui ne passent pas par 0, on obtient une infinité d’éléments analytiques différents (face=F0019 漣 1, Tn ), n 捻 Z, où Tn est la détermination du logarithme dans D(face=F0019 漣 1, 0) telle que:
si on considère aussi, à partir de ce même élément (1, S), les prolongements analytiques le long de tous les chemins d’origine 1 et d’extrémité 漣 1 qui ne passent pas par 0, on obtient une infinité d’éléments analytiques différents (face=F0019 漣 1, Tn ), n 捻 Z, où Tn est la détermination du logarithme dans D(face=F0019 漣 1, 0) telle que: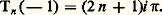 Les problèmes que nous rencontrons ici et qui constituent ce qu’on appelait improprement la théorie des «fonctions» multiformes trouvent leur véritable cadre dans la théorie des surfaces de Riemann.Surface de Riemann d’un élément analytiqueSoit (a , S), un élément analytique de centre a , considérons l’ensemble X des éléments analytiques (b , T) qui sont des prolongements analytiques de (a , S) le long de chemins du plan complexe. On désignera par p : XC l’application de «projection» qui à (b , T) 捻 X fait correspondre b .Soit B0 = (b 0, 0) 捻 X un élément analytique du disque de convergence D0 et désignons par V(B0) l’ensemble des éléments analytiques centrés dans D0 qui sont des prolongements analytiques directs de B0 (ce sont les éléments analytiques déterminés par la fonction 0 analytique dans D0). La restriction p 0 de la projection p à V(B0) est une bijection de V(B0) sur D0 au moyen de laquelle on peut «transporter» sur V(B0) la structure analytique du disque D0. On définira ainsi, à partir de ceux de D0, les ouverts de V(B0); une fonction à valeurs complexes définie dans V(B0) sera dite analytique si f 獵 p 0-1 est analytique dans D0 (fig. 9): par exemple p est analytique; de même, l’application qui à (b , T) associe T(b ) est analytique.Par recollement, on a ainsi muni X d’une structure de variété analytique complexe de dimension (complexe) 1; le couple (X, p ) s’appelle la surface de Riemann de l’élément analytique (a , S). On dit aussi que c’est une surface de Riemann au-dessus de l’ouvert G = p (X); pour des exemples et une introduction à l’étude des surfaces de Riemann, nous renvoyons à l’article suivant, qui traite de la représentation conforme. Signalons cependant pour terminer le principe de monodromie , qui affirme que, si G est simplement connexe, alors p est une bijection, donc X est analytiquement isomorphe à G.8. Théorèmes d’approximationLe théorème de Runge affirme que, si U est un ouvert du plan complexe et A un ensemble ayant un point dans chaque composante connexe du complémentaire de U, alors toute fonction f analytique dans U est limite uniforme sur tout compact dans U d’une suite de fractions rationnelles dont les pôles appartiennent à A. Dans le cas particulier où U est borné et «sans trous», ce qui veut dire que C 漣 U est connexe, alors f est limite uniforme sur tout compact d’une suite de polynômes.Le théorème de S. N. Mergelyan est un résultat difficile, publié en 1954; il affirme que, si K est un compact du plan complexe, de complémentaire connexe, toute fonction continue sur K, holomorphe dans l’intérieur de K, est limite uniforme sur K de polynômes.9. Théorèmes de décompositionThéorème de factorisation de WeierstrassLa théorie de Weierstrass a pour objet de généraliser aux fonctions entières (c’est-à-dire analytiques dans tout le plan complexe) le théorème de d’Alembert-Gauss.Les zéros non nuls d’une fonction entière peuvent être rangés en une suite (z n ), chaque zéro étant répété dans cette suite un nombre de fois égal à sa multiplicité, telle que |z n | soit une suite croissante, car tout disque ne contient qu’un nombre fini de tels zéros.D’une part, étant donné une telle suite (z n ), il existe une fonction entière F associée à cette suite de zéros. L’idée la plus simple consiste à poser:
Les problèmes que nous rencontrons ici et qui constituent ce qu’on appelait improprement la théorie des «fonctions» multiformes trouvent leur véritable cadre dans la théorie des surfaces de Riemann.Surface de Riemann d’un élément analytiqueSoit (a , S), un élément analytique de centre a , considérons l’ensemble X des éléments analytiques (b , T) qui sont des prolongements analytiques de (a , S) le long de chemins du plan complexe. On désignera par p : XC l’application de «projection» qui à (b , T) 捻 X fait correspondre b .Soit B0 = (b 0, 0) 捻 X un élément analytique du disque de convergence D0 et désignons par V(B0) l’ensemble des éléments analytiques centrés dans D0 qui sont des prolongements analytiques directs de B0 (ce sont les éléments analytiques déterminés par la fonction 0 analytique dans D0). La restriction p 0 de la projection p à V(B0) est une bijection de V(B0) sur D0 au moyen de laquelle on peut «transporter» sur V(B0) la structure analytique du disque D0. On définira ainsi, à partir de ceux de D0, les ouverts de V(B0); une fonction à valeurs complexes définie dans V(B0) sera dite analytique si f 獵 p 0-1 est analytique dans D0 (fig. 9): par exemple p est analytique; de même, l’application qui à (b , T) associe T(b ) est analytique.Par recollement, on a ainsi muni X d’une structure de variété analytique complexe de dimension (complexe) 1; le couple (X, p ) s’appelle la surface de Riemann de l’élément analytique (a , S). On dit aussi que c’est une surface de Riemann au-dessus de l’ouvert G = p (X); pour des exemples et une introduction à l’étude des surfaces de Riemann, nous renvoyons à l’article suivant, qui traite de la représentation conforme. Signalons cependant pour terminer le principe de monodromie , qui affirme que, si G est simplement connexe, alors p est une bijection, donc X est analytiquement isomorphe à G.8. Théorèmes d’approximationLe théorème de Runge affirme que, si U est un ouvert du plan complexe et A un ensemble ayant un point dans chaque composante connexe du complémentaire de U, alors toute fonction f analytique dans U est limite uniforme sur tout compact dans U d’une suite de fractions rationnelles dont les pôles appartiennent à A. Dans le cas particulier où U est borné et «sans trous», ce qui veut dire que C 漣 U est connexe, alors f est limite uniforme sur tout compact d’une suite de polynômes.Le théorème de S. N. Mergelyan est un résultat difficile, publié en 1954; il affirme que, si K est un compact du plan complexe, de complémentaire connexe, toute fonction continue sur K, holomorphe dans l’intérieur de K, est limite uniforme sur K de polynômes.9. Théorèmes de décompositionThéorème de factorisation de WeierstrassLa théorie de Weierstrass a pour objet de généraliser aux fonctions entières (c’est-à-dire analytiques dans tout le plan complexe) le théorème de d’Alembert-Gauss.Les zéros non nuls d’une fonction entière peuvent être rangés en une suite (z n ), chaque zéro étant répété dans cette suite un nombre de fois égal à sa multiplicité, telle que |z n | soit une suite croissante, car tout disque ne contient qu’un nombre fini de tels zéros.D’une part, étant donné une telle suite (z n ), il existe une fonction entière F associée à cette suite de zéros. L’idée la plus simple consiste à poser: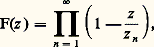 mais ce produit ne converge que si la série 1/|z n | est convergente. Dans le cas général, il faut «corriger» le facteur (1 漣 z /z n ) par un facteur exponentiel. On est ainsi conduit à introduire les fonctions suivantes, dites facteurs primaires:
mais ce produit ne converge que si la série 1/|z n | est convergente. Dans le cas général, il faut «corriger» le facteur (1 漣 z /z n ) par un facteur exponentiel. On est ainsi conduit à introduire les fonctions suivantes, dites facteurs primaires: Il est alors possible de trouver une suite (p n ) d’entiers positifs tels que le produit infini:
Il est alors possible de trouver une suite (p n ) d’entiers positifs tels que le produit infini: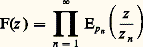 soit normalement convergent sur tout compact de C, ce qui fournit une fonction qui convient.Inversement, soit f une fonction entière, (z n ) la suite de ses zéros non nuls et k l’ordre de multiplicité de la racine 0. Alors, la fonction f /z k F est une fonction entière qui ne s’annule pas, donc de la forme e g , où g est entière.Finalement, on a:
soit normalement convergent sur tout compact de C, ce qui fournit une fonction qui convient.Inversement, soit f une fonction entière, (z n ) la suite de ses zéros non nuls et k l’ordre de multiplicité de la racine 0. Alors, la fonction f /z k F est une fonction entière qui ne s’annule pas, donc de la forme e g , où g est entière.Finalement, on a: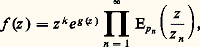 décomposition de f en facteurs primaires.On peut étendre ce résultat à un ouvert U simplement connexe de C: Soit A un sous-ensemble discret (donc nécessairement dénombrable) de U et associons à chaque point a 捻 A une «multiplicité» n a qui soit un entier positif; on peut alors montrer qu’il existe une fonction analytique dans U dont les zéros sont exactement les points de A, avec les multiplicités correspondantes. Il en résulte que, si h est une fonction méromorphe dans U, alors elle peut s’écrire, dans U tout entier et non pas seulement localement, comme quotient de deux fonctions analytiques.Théorème de Mittag-LefflerLa théorie de Mittag-Leffler a pour objet de généraliser aux fonctions méromorphes dans C la décomposition en éléments simples des fractions rationnelles.Soit f une fonction méromorphe dans C et (z n ) la suite de ses pôles distincts, y compris éventuellement 0, organisée par module croissant, et soit:
décomposition de f en facteurs primaires.On peut étendre ce résultat à un ouvert U simplement connexe de C: Soit A un sous-ensemble discret (donc nécessairement dénombrable) de U et associons à chaque point a 捻 A une «multiplicité» n a qui soit un entier positif; on peut alors montrer qu’il existe une fonction analytique dans U dont les zéros sont exactement les points de A, avec les multiplicités correspondantes. Il en résulte que, si h est une fonction méromorphe dans U, alors elle peut s’écrire, dans U tout entier et non pas seulement localement, comme quotient de deux fonctions analytiques.Théorème de Mittag-LefflerLa théorie de Mittag-Leffler a pour objet de généraliser aux fonctions méromorphes dans C la décomposition en éléments simples des fractions rationnelles.Soit f une fonction méromorphe dans C et (z n ) la suite de ses pôles distincts, y compris éventuellement 0, organisée par module croissant, et soit: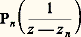 la partie principale relative au pôle z n . Par un procédé correctif analogue à celui qui est employé dans le théorème de Weierstrass, on montre qu’il existe des polynômes Qn tels que la série:
la partie principale relative au pôle z n . Par un procédé correctif analogue à celui qui est employé dans le théorème de Weierstrass, on montre qu’il existe des polynômes Qn tels que la série: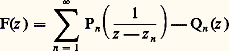 soit normalement convergente sur tout compact de C 漣 S, où S est l’ensemble des pôles.Dans ces conditions, la fonction:
soit normalement convergente sur tout compact de C 漣 S, où S est l’ensemble des pôles.Dans ces conditions, la fonction: est une fonction entière.On peut étendre ce résultat à un ouvert quelconque de C.Les théorèmes de Weierstrass et de Mittag-Leffler s’appliquent notamment aux développements eulériens des fonctions transcendantes élémentaires (cf. EXPONENTIELLE ET LOGARITHME, chap. 5), au développement de la fonction gamma (cf. fonction GAMMA) et à la construction des fonctions elliptiques (cf. FONCTIONS ANALYTIQUES-Fonctions elliptiques et modulaire).
est une fonction entière.On peut étendre ce résultat à un ouvert quelconque de C.Les théorèmes de Weierstrass et de Mittag-Leffler s’appliquent notamment aux développements eulériens des fonctions transcendantes élémentaires (cf. EXPONENTIELLE ET LOGARITHME, chap. 5), au développement de la fonction gamma (cf. fonction GAMMA) et à la construction des fonctions elliptiques (cf. FONCTIONS ANALYTIQUES-Fonctions elliptiques et modulaire).
Encyclopédie Universelle. 2012.
